Sets

Definition: A set is an onordered collection of items with something in common 

Set vocabulary

Element - an item contained within a set

Order - The number of items in a set

Subset - A set where all the elements are also contained in another set

Null set - A set not containing any elements

Universal set - All possible values for the element, which are relevant. 

Disjoint sets - No element between either set is shared. 

Set notation

Notation	Meaning
$x\in A$	The element x is contained in the set A
$x\notin A$	The element x is not contained in the set A
$n\left(A\right)=x$	The order of the set is x
$A\subset B$	Set A is a subset of set B
$A\cap B$	The intersection between set A and B. Contains all shared elements between both sets.
$A\cup B$	The union between set A and B. Contains all elements from both sets.
$A\cup B = \varnothing$	A and B are disjoint sets.
$\varnothing$	A null set or empty set
$\xi$ or $U$	The universe

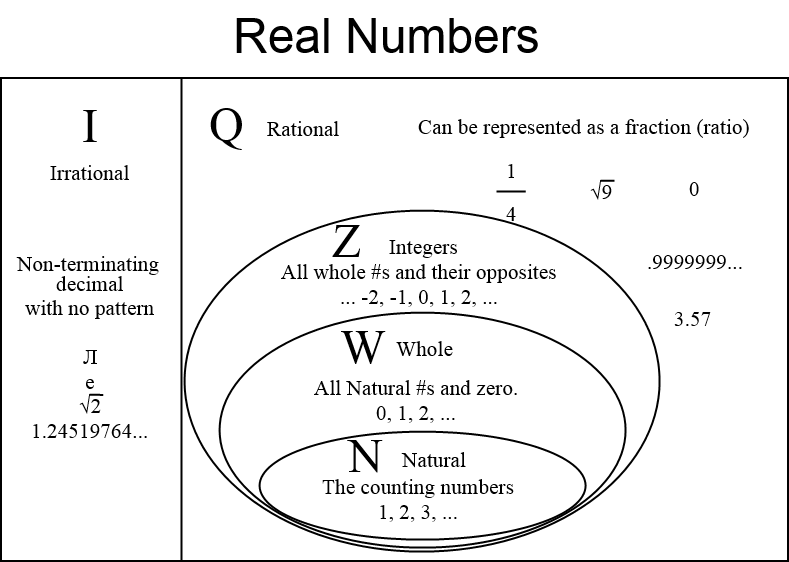
Number Sets

There are different sytems in which we use to classify numbers and these are called the number sets. 

Number set	Description	Examples	Symbol
Real numbers	Any number which can be found on the number line.	$\mathrm{\pi }, -1, 5 , \sqrt{2}, \frac{7}{5}$	$\mathrm{ℝ}$
Rational numbers	Any number which can be expressed by a fraction of two integers.	$-5 , \frac{3}{5}, 8 , \frac{2}{17}$	$\mathrm{\mathbb{Q}}$
Irrational numbers	Any number which can't be expressed with a fraction. They have infinite non-repeating digts after the decimal place.	$\sqrt{2},\pi , e , \sqrt{17}$	$\mathrm{ℝ}/\mathrm{\mathbb{Q}}$
Integers	Any numbers which can be expressed without decimals or fractions.	$8 , 0 , -100$	$\mathrm{\mathbb{Z}}$
Whole numbers	Positive integers including 0	$0 , 1 , 2 , 3$	$\mathbb{W}$
Natural numbers	Positive integers excluding 0	$1 , 2, 3 , 4$	$\mathrm{\mathbb{N}}$
Negative integers	All integers less than 0	$-1 , -2, -3$	${\mathrm{\mathbb{Z}}}^{-}$

Diagram

Exponents

An Exponent is the number that a number is raised to. This is also referred to as an indice. 

Rules of exponents

$a^m\times a^n=a^{m+n}$

$a^m÷a^n=a^{m-n}$

${\left(a^m\right)}^n= a^{mn}$

$a^{-n}=\frac{1}{a^n}$

$a^{\frac{1}{n}}=\sqrt[n]{a}$

$a^0=1$

Fractional exponents

A fractional exponent means that a number is being raised to the power of a fraction. It takes the form below:

Form: $a^{\frac{n}{m}}$

Example: $2^{\frac{2}{3}}$

Simplifying fractional exponents

We can easily simplify fractional indices by using the rules of indices.

$a^{\frac{n}{m}}=(a^n{)}^{\frac{1}{m}} = \sqrt[m]{a^n}$

Logarithims

A logarithm is simply an algorithm which take an input and a base and outputs the exponent needed to raise the base by to produce the input.

How to make a logarithm

A logarithm can be written using the form shown below:

${\log }_n\left(a\right)=b$

n - the base

a - the input

b - the output

For example: ${\log }_2\left(16\right)=4$

Logarithm rules

Name	Rule
Product rule	${\log }_b\left(mn\right)= {\log }_b\left(m\right)+{\log }_b\left(n\right)$
Quotient rule	${\log }_b\left(\frac{m}{n}\right)= {\log }_b\left(m\right)-{\log }_b\left(n\right)$
Power rule	${\log }_b\left(m^n\right)=n· {\log }_b\left(m\right)$
Change of base rule	${\log }_a\left(x\right)= \frac{{\log }_b\left(x\right)}{{\log }_b\left(a\right)}$
Equality rule	$if {\log }_a\left(x\right)= {\log }_a\left(y\right), then x = y$

View count: 6121