Glossary

Term	Definition
Postulate	Something that is so obviously true, you accept it as fact, and it needs no proof. E.g SAS postulate, RHS postulate, etc...

Angle Properties

Angle names

 

In geometry an angle can be one of four types of angles:

• Acute: Less than 90 degrees
• Right angle: Exactly 90 degrees
• Obtuse: More than 90 degrees
• Reflex: More than 180 degrees

Angles in intersecting lines

Angle pairs	Description	Diagram
Opposite / Vertical	Angles opposite to each other around the intersection of two lines are equal.
Adjacent	Angles which are next to each other
Supplementary	Angles which add up to 180°. The diagram shows an adjacent and supplementary angle pair.
Alternate	Angles on either side of the intersecting line of two parallel lines are equal. They must be on the interior of the parallel lines.
Corresponding	Angles on the same side of the  intersecting line of two parallel lines are equal. One angle is in the interior while one is on the exterior.

Angles in triangles

These are postulates: 

1. Angles in a triangle add up to 180°
2. The exterior angle of any side is equal to the sum of the other non-adjacent interior angles.

Angles in polygons

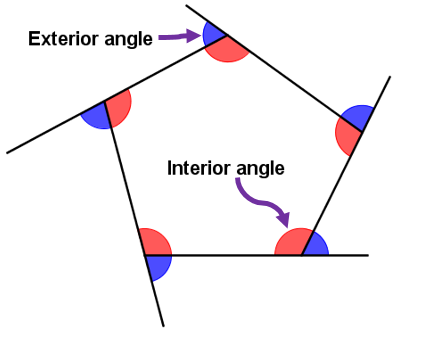
Interior and exterior angles

• Interior angle: The angles made between two sides in the interior of the polygon
• Exterior angle: The angle made between one of the sides of the polygon and an extended side.

Exterior angle = 180°- interior angle

Sum of angles

• Sum of interior angles = $(n-2)\times 180°$
• Sum of exterior angles = $360°$

The sum of interior angles formula comes form the fact that if you divide a polygon into triangles, there will be the same numbe rof triangles as the number of sides minus two. We already know all the angles in a triangle add up to 180°, so to get the sum of interior angles we just multiply the number of triangles by 180°.

$$\begin{gathered} \mathit{\#}\mathit{ }triangles\mathit{=\; (}n\mathit{-2)} \\ Sum\mathit{ }of\mathit{ }triangle\mathit{ }angles\mathit{=}\mathit{ }\mathit{180°} \\ Sum\mathit{ }of\mathit{ }interior\mathit{ }angles\mathit{ }\mathit{=}\mathit{ }\mathit{ }\mathit{\#}triangles\mathit{ }\mathit{\times }\mathit{ }sum\mathit{ }of\mathit{ }triangle\mathit{ }angles\mathit{ }\mathit{=}\mathit{ }\mathit{(}n\mathit{-}\mathit{2}\mathit{)}\mathit{\times }\mathit{180}\mathit{°} \end{gathered}$$

Size of each angle in a regular polygon

• Each interior angle = $(n-2)\times 180°/n$
• Each exterior angle = $360°/n$ 

These values are given by taking the sum of angles and dividing by number of sides. 

Similar Triangles

Definition: When two shapes have the same interior angles but different lengths of sides. It is effectively two shapes that are just enlargements of some sort of each other.

Finding missing lengths with similar triangles

If 2 triangles are similar then the ratio of any correspoding side lengths will be the same for any pair. 

This means that given a pair of similar triangles, if all the side lengths of the smaller triangle are known then the side lengths of the larger triangle can be found using the scale factor.

How to find missing lengths using similar triangles:

1. Identify two similar sides in the different shapes
2. Divide the larger side by the smaller side to find the scale factor or ratio.
3. Using this ratio, multiply the smaller triangles sides by the ratio factor to find the missing lengths in the big triangle.

Note: It is important to keep track of which sides of the triangle or shape are similar because this rule only works if you use similar sides.

Congruent triangles

If two triangles are congruent this means they are exactly the same. If two traingles are congruent, all their side lengths and angles will be the same.

Symbol for congruency

The symbol for congruency is an equals sign with an extra line above it.

$\equiv$

Triangle Congruence Postulates

To figure out if two triangles are congruent when a question does not give all the side lengths and angles you can use the triangle congruence postulates. 

Postulate	Condition	Diagram
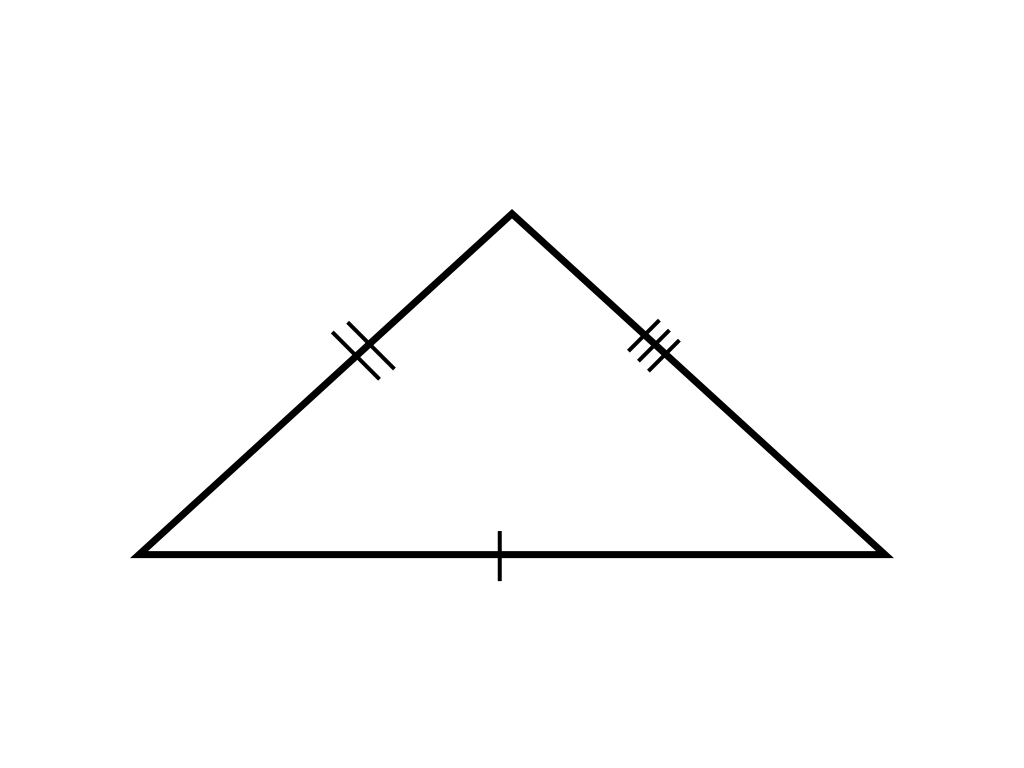
SSS Postulate	When all corresponding sides are equal in length.
AAS/ASA Postulate	When two angles and one side are given and are equal.
SAS Postulate	When two sides and one angle are given and are equal.
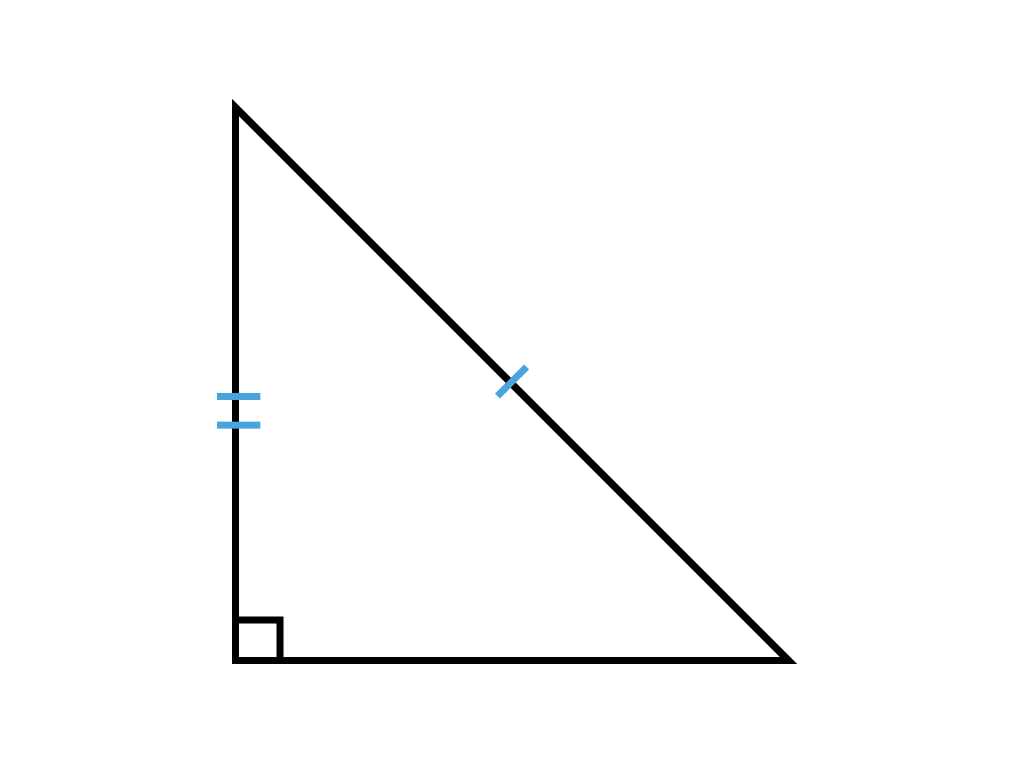
RHS Postulate	For right-angled triangles, the hypotenuses and 0 other pairs of sides are equal.

Special triangles

30-60-90 -triangle

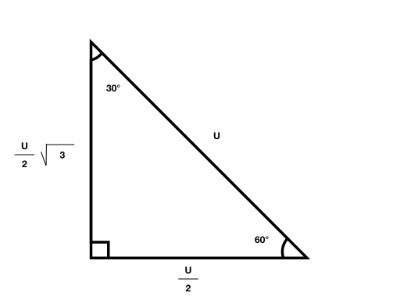
This is a triangle where the angles are 30, 60 and 90.

This is useful because, in all 30-60-90 triangles, you know the ratio of the lengths of sides so if you know one side of the triangle, you can calculate the other sides.

For example, if you know the shorter side:

• The hypotenuse = shorter side * 2
• Longer Leg = Shorter Side * 3

90-45-45 - triangle

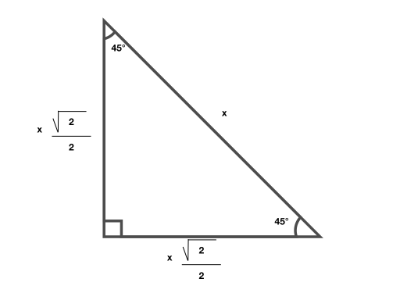
This is a triangle where the angles are 90, 45 and 45

This is useful because, in all 90-45-45 triangles, you know the ratio of the lengths of sides so if you know one side of the triangle, you can calculate the other sides.

View count: 6778