Intro to functions

Functions are a way of describing a special relationship between an input and an output variable.

It is like a set of rules for how to transform a number.

It is mainly written as f(x), such that x is the input vairable.

Plotting a function

if the input variable represents the x-axis and the output the y axis of a coordinate plane then a function can be plotted on a graph. To do this by hand plot a 4-5 points on the graph and then join them with a smooth line. 

 

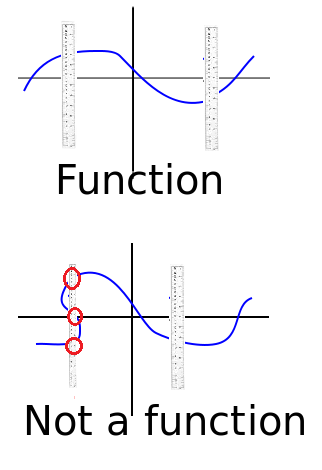
Vertical line test

A function takes a single input and give a single output. If there is more than one outcome the equation is not a function. 

To test  if an equation is a function, you can perform the verticla line test. To do this graph the function and move a vertical line, such as a ruler horizontally across the graph. If the vertical line touches more than one point, then these points share the same input and it is not a function. If no two points touch the vertical line at the same time the equation has passed the test and is a function

Terms to describe functions

Term	Examples	Definition
Monomial	2x, m, 3,	A number, a variable or a product of numbers and variables.
Polynomial	2x+5, k2+8	Any function that connects coefficents and variables only with the operations of multiplicaiton, devison, addition and subtraction.
Degree of a polynomial	x4+3x2-2x	The greatest exponent in a function with a variable base.
Leading Coefficient	3x, $\frac{\mathbf{1}}{\mathbf{4}}x$	Coefficient of the term with the highest exponent.
Turning Point		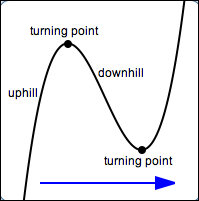A point on a graph where the gradient changes from positive to negative or from negative to positive.

Families of Functions

Name of function	General form	Example	Characteristics
Linear	ax+b	2x -1	The highest power/exponent of any variable in the function is 1.
Quadratic	ax2+bx+c	x2 + x -5	The highest power/exponent of any variable in the function is 2.
Cubic	ax3+bx2+cx+d	4x^3 -x^2	The highest power/exponent of any variable in the function is 3.
Rational	$\frac{P\left(x\right)}{Q\left(x\right)}$	$\frac{2x^2+1}{x-3}$	Devision is used as an operator
Exponential	$a^{x-b}+c$	f(x)=2^(x-1) -5	There is a variable in the exponent.
Logarithmic	${\log }_a\left(P\left(x\right)\right)$	f(x)=log(2x-3)	It has a log in it.
Trigonometric	$a*trig(x-b)+c$	f(x)=Cos(x)	It has a trigonometric ratio in it.

 

Linear functions

Function

$f\left(x\right)=mx+c$

m = determines the gradient/steepness of the line

c = changes y-intercept

x = input number

Functions for parallel and perpendicular lines

Parallel Lines:  have same gradient but different y-intercepts

Perpendicular line: has a negative and flipped gradient (this also affect and determines the y-intercepts)

Exponential Functions

Function

$f\mathit{\left(}x\mathit{\right)}\mathit{=}a{b}^{zx\mathit{ }\mathit{+}c}\mathit{+}d$

a= Determines reflection on x-axis

b= Changes the gradient/steepness of the line

c= Transforms the line on the x-axis

d= Changes horizontal asymptote and y-intercept

x= Input number

z= Determines reflection on y-axis.

 

Domain and Range

Definition: The domain is the restrictions of the x values.

E.g. Domain is: x > 0, x € ℝ

Range

The set of all possible outputs of a function (z-values on the graph) is called the range of a function.

E.g: Range is: 1 < y < 3, y = ℝ

Things that restrict the Domain and range:

1. You cannot divide by zero.
2. You cannot take the square root of a negative number.
3. You cannot take the logarithm of a negative number or zero.

Transforming functions

Sin, Cos functions

Basic structure of the functions:

f(x)=a(x-h)2+k

f(x)=asin (bx)+c

View count: 6287