Help us by clicking edit and filling in the topics

Linear equations

Solving by rearranging

When solving any equation all you are trying to do is get the variable on it's own on one side of the equation. 

	Method	Example
1	Put all terms containing the variable on one side and the constants on the other	$6x+8=20\to 6x=12$
2	Divide by the coefficent infront of x	\(\frac{6x}{6}=\frac{12}{6}\rightarrow x=2\)

Solve by graphing

To do this rearrange the function so the left side is 0, and graph the function. 

The x intercept, is the solution to the equation. 

 

Quadratic

Facto

Simulataneous equations

What are they?

If given an equation with more than one unknown, it is impossible to solve for both variables as there are an infinite number of possiblities. Inorder to solve this you need another equation equal to it, this is called a simultaneus equation.

In a simultaneus equation, there is only one combination of unknowns which will result in both equations being equal and because of this we can solve for the unknowns. 

Solving with a graphics calculator

A simultaneus equation finds the point where the two equations meet, known as the intersection. We can find this intersection by graphing both equations on a calculator

Note: In MYP these simultaneus equations will always be linear. 

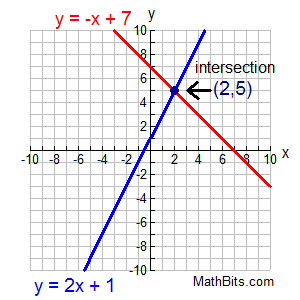
After graphing the equations you can find the x and y value of the intersection, by going to: Menu - Analyse Graph - Intersection and selecting the two graphs. 

Solving with elimination

To solve simultaneus equations through elimination, you need to subtract or add one equation from the other so that you eliminate one of the variables and are left with only one.

	Method	Example
1	Make both equations have the same form.	$\left\{\begin{array}{l}3x+3=-4y\\ 2x+2y =6\end{array}\right.\to \left\{\begin{array}{l}3x+4y=-3\\ 2x+2y =6\end{array}\right.$
2	Multiply one or both equations so that the coefficents match between a variable in both equations.	$\left\{\begin{array}{l}3x+4y = -3\\ 2\times (2x+2y) = 2\times 6\end{array}\right.\to \left\{\begin{array}{l}3x+4y = -3\\ 4x+4y = 12\end{array}\right.$
3	Subtract or add the equations so that the variable with the same coefficents is eliminated.	$\begin{array}{cc}& 3x+4y = -3\\ -& 4x+4y = 12\end{array} \to -x=-15$
4	Solve for x	$x=15$
5	Subsitute value for x back in to one of the equations and solve for y.	$$\begin{gathered} 2·\left(15\right)+2y =6 \\ y = \frac{6-30}{2} \\ y=-12 \end{gathered}$$

Inequalities

 

View count: 4461