Simple Harmonic Motion (SMH)
Conditions of Simple Harmonic Motion
- There is a fixed cyclical path.
- There is a central equilibrium point.
- The motion repeats at equal time periods (periodic).
- Displacement from equilibrium, velocity, and acceleration change continuously.
- There is a restoring force directed toward the equilibrium point.
Describing Simple Harmonic Motion with Hooke's law
A simple example of Simple Harmonic Motion is a mass, attached to a spring, hanging from a ceiling. This can be calculated using Hooke's Law, F = -kX.
The equilibrium position here is when the net force is 0. This occurs when the sum of the weight vector and the spring tension (the restoring force) vector is equal to zero.
Position–time and velocity-time graphs of an object in SHM.
As the object moves to a larger displacement, the acceleration from the restoring force becomes correspondingly larger. Mathematically, this is expressed as: \(\qquad\qquad a \propto - x\)
For springs this relation is called Hooke's law, after its discoverer, Robert Hooke; a contemporary (and rival) of Isaac Newton in the late 17th century.
\(\qquad\qquad F_\text{net} \propto - x\)
or
\(\qquad\qquad F_\text{net} = -kx\)
where \(k\) is a constant.
Remember that many forces can act as restoring forces. Not all restoring forces are linear and they may produce oscillations, but the motion will not be SHM.
Definition of Simple Harmonic Motion
Simple harmonic motion is defined as motion arising from acceleration of an object that is proportional to its displacement from a fixed equilibrium point (rest position) and directed toward that point.
Alternatively, simple harmonic motion is defined as motion arising from a linear restoring force directed to a fixed equilibrium point
Remember that the amplitude of SHM is the maximum displacement from equilibrium and that you are not required to know the full mathematical analysis behind SHM.
Frequency
The time taken for one cycle of oscillation is the period \(T\) and is related to the number of cycles per unit time or frequency \(f\). They are related by \(f = \dfrac{1}{T}\) (equivalent to \(T = \dfrac{1}{f}\) in your formula booklet). The unit for frequency is hertz \((Hz)\) or \(\mathrm s^{-1}\).
SHM and phase shifts
Two sinusoidal curves of equal period have a phase shift that translates one curve relative to the other in time, expressed as a fraction of a cycle, or as an angle in radians or degrees.
Deriving the SHM equations (optional)
Displacement as a function of time
X(t)=X0*sin(wt) or X(t)=,X0cos(wt), where X0 is amplitude, t is time, and w is angular velocity.
The first equation is used if the motion starts at equilibrium.
The second equation is used if the motion starts at the maximum amplitude.
Velocity as a function of time
The motions for velocity as functions of time can easily be derived with calculus. Remember that velocity is the derivative of displacement with respect to time. So using the chain rule we get
V(t)=wX0cos(wt) or V(t)=-wX0sin(wt).
The first equation is used if the motion starts at equilibrium.
The second equation is used if the motion starts at the maximum amplitude.
If you have covered calculus in maths, it's easy to understand how these equations are obtained, and it provides intuition behind the motion as a function of time.
Acceleration as a function of time
Now by taking the second derivative of displacement with respect to time, we can find a(t), acceleration as a function of time
a(t)=-w2X0sin(wt) or a(t)=-w2X0cos(wt).
Acceleration as a function of displacement
By comparing the equations for displacement, and the equations for acceleration, we can obtain an equation for acceleration as a function of displacement. a(X) = -(w2)X. From Newton's second law, F=ma, we can find F/m = -(w2)X. Solving for F gives us F = -(X2)Xm. This again gives us the relation between F and X, F-X, and is a useful formula to find the strength of the force as a function of displacement.
The energy in Simple Harmonic Motion
As with anything, the total energy is the sum of the kinetic and potential energy of the system. In this system, we are assuming that no energy enters and leaves the system, so energy is conserved. Intuitively, the sum of kinetic and potential must always remain the same.
What is a Wave?
A wave can be described as a fluctuation in energy travelling that travels from one location to another. Usually, (with the exception of things like electromagnetic radiation), waves travel through a medium, without the actual movement of matter. The matter itself is only temporarily displaced from its rest position, due to the change in energy.
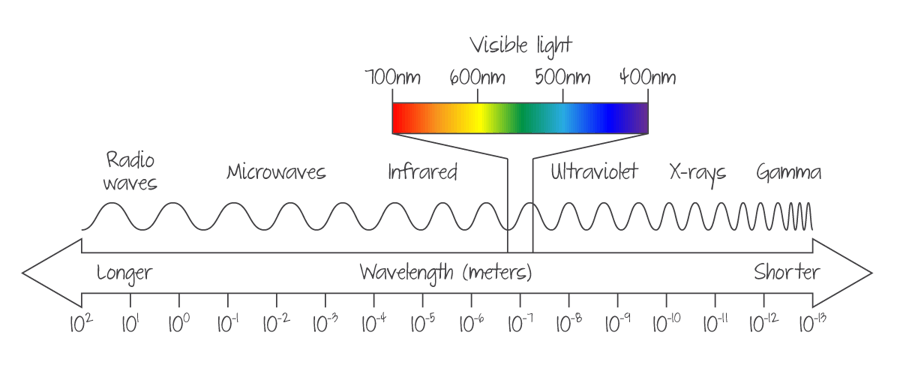
You must memorise the seven areas of the electromagnetic spectrum and their approximate wavelengths as shown
Types of travelling waves
Longitudinal Waves
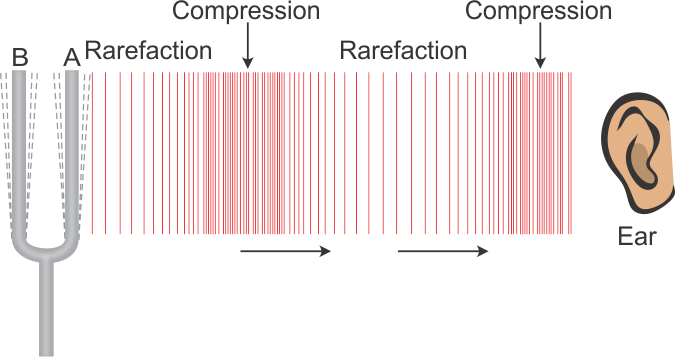
Longitudinal waves are waves that oscillate parallel to the direction of motion of the wave. An example of a longitudinal wave is sound. Here, the oscillations are compressions and rarefactions of the air that move outwards away from the source. This is shown in the diagram below, where the soundwaves move towards the ear, and the compressions and rarefactions happen in that same direction.
Transverse Waves
Transverse waves are waves that oscillate perpendicular to the direction of motion of the wave. You can view both types of waves in the model below (use right-click to rotate and scroll to zoom).
Wave Properties
For mechanical waves:
- The wave propagates energy through the medium, but the wave does not oscillate.
- The particles of the medium oscillate, but the particles do not propagate through the medium.
The key distinction of an electromagnetic wave compared to a mechanical wave is that no medium is necessary for it to propagate; it can move through empty space devoid of material. The reason for this is that the wave is a coupled electric and magnetic field disturbance that varies in time, and these fields can exist in a vacuum. No mechanical energy is involved.
Describing Waves
All travelling waves can be described and differentiated with certain mathematical characteristics. These characteristics are listed below.

Crest: The maximum displacement of the wave from equilibrium, measured in meters.
Trough: The maximum (-) displacement of the wave from equilibrium, measured in meters.
Wavelength: The distance between one point on a wave, and the nearest point on the wave that is perfectly in phase with it, measured in meters. Sometimes referred to as lambda, written with the greek symbol.
Period: The amount of time it takes for a wave to complete one full oscillation. Measured in seconds, written with a T.
Frequency: The number of oscillations per second. Measured in hertz (s-1). Written with a lowercase f. It is equivalent to the reciprocal of the period. (The wave frequency is determined by the frequency of the oscillating energy source that produces the wave.)
The speed \(v\) of a travelling wave in a medium is related to frequency \(f\) (or period \(T\)) and wavelength \(\lambda\) by \(v= \dfrac{\lambda}{T} = f\lambda\)
In a question relating wave speed, frequency (or period), and wavelength, using \(v= d / t\) is worth no credit.
Graphically describing a wave
The most useful way of graphing a travelling wave is by graphing its displacement from equilibrium with time, as shown in the diagram below.
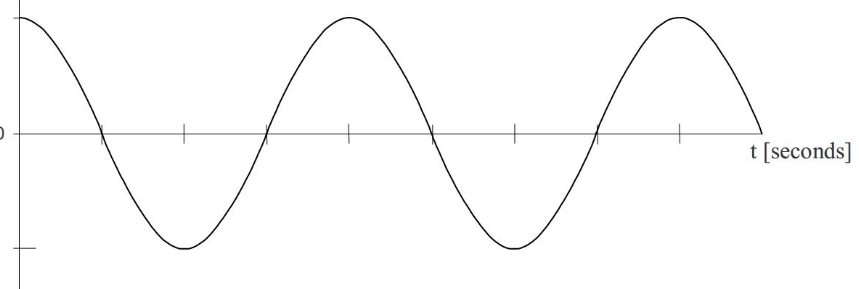
From this, we can see the amplitude of the wave. This is the maximum displacement from the x-axis. It is also possible to find the period. The period is the amount of time for one full oscillation, so it doesn't matter which two points are used on the graph to measure this, so long as they are in phase, and are part of adjacent oscillations.
However, waves can also be graphed as the variation of displacement from equilibrium as a wave moves away from its source.
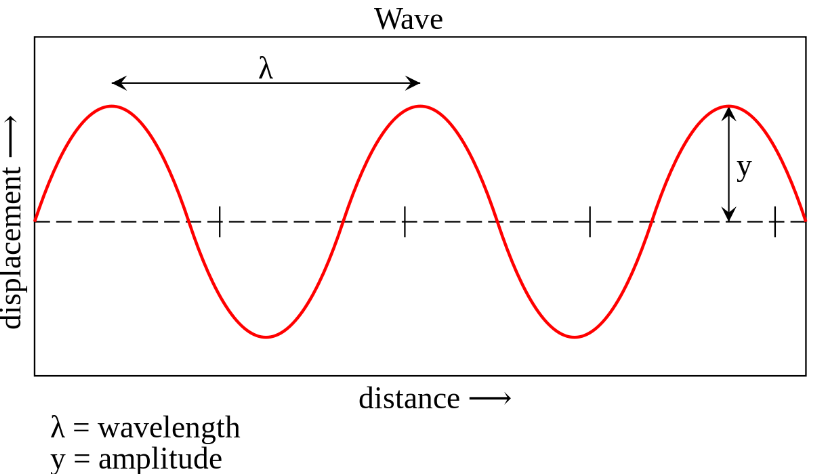
From this graph here, we can ascertain certain information about the wave. Although with this, we can't find the period and frequency of the wave, we can now find the wavelength, which is also a very important wave property. The easiest way of measuring it is the distance between two adjacent crests/troughs, however, it can be any two points, so long as they are in phase and are in adjacent oscillations to each other.
Exam tip
Use precise scientific terminology when describing sound.
| Scientific Terminology | Music Terminology (do not use) |
| Frequency | Pitch or Note |
| Amplitude | Volume |
Speed of Sound
The value of the speed of sound depends on the medium in which the sound wave travels. The simplest way to determine the speed of sound to record the time interval for a sound pulse travelling from one point to another. This involves detecting a sound pulse and starting a timer, then detecting the pulse again either at a different location having a known-separation from the first, or by reflecting the sound pulse from a wall a known distance away, and stopping the timer.

Use this to determine the speed of sound in air. The application on the mobile phone measures a time interval between clap and echo of \(
Ans: \(350ms^-1\)
A common error is to only use the "one-way" path length as the total travelled distance in echo-type problems. Make sure that you account for the sound wave travelling to the wall or object and back to the observer.
Wave Characteristics
3D Diagrams of Wavefronts and Rays
To understand what a wave is really like, we need to go further than just imagining them in 1 dimension, as we have previously had. The best way to do this is to draw them. The diagram below shows a wave moving out from its source.
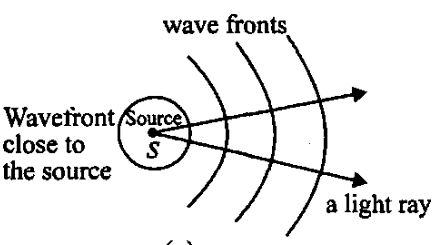
Wavefronts represent two points of a wave that are in phase. Often, they are crests of troughs. They are useful because they allow us to depict waves without actually having to draw one.
Rays represent the direction of the wave. Rays should always be perpendicular to wavefronts, no matter what. They always move outwards and away from the source.
Diffraction
Diffraction is the bending of waves around corners of an opening or obstacle, into the geometrical shadow of the obstacle. Diffraction is produced by a limited part of a wavefront.
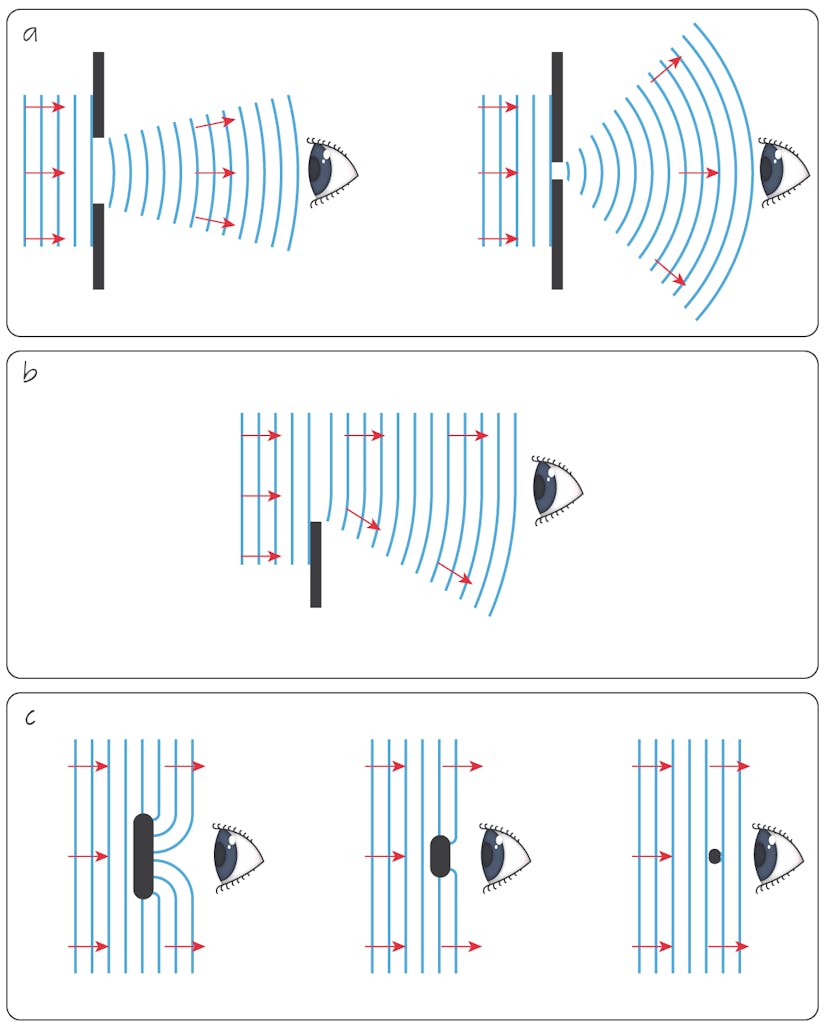
Diffraction effects are most significant when the wavelength \(\lambda\) is comparable to the opening or obstacle size, \(w\), that is, when \(\dfrac{ \lambda} {w} \approx 1\).
Rays
Rays are useful representations for drawing simple, uncluttered optical constructions that omit the many details of wavefronts and that use shortcuts based on known optical principles. Notice how much cleaner the representations are, though lacking in the "why?" or "how?" of what we see. Ray diagrams are especially useful for understanding combinations of lenses or reflectors.

Wave Intensity
In theory, the total energy of a wave shouldn't change as it moves outwards from the source. However, intuition tells us something does. When someone is speaking, it's easier to hear them when they're closer to you. If you shine a torch at a cliff 2 kilometres away, you won't see the torchlight on the cliff. But if you shine it at a wall right next to you, you will. So if total energy doesn't change with distance, then why does this happen?
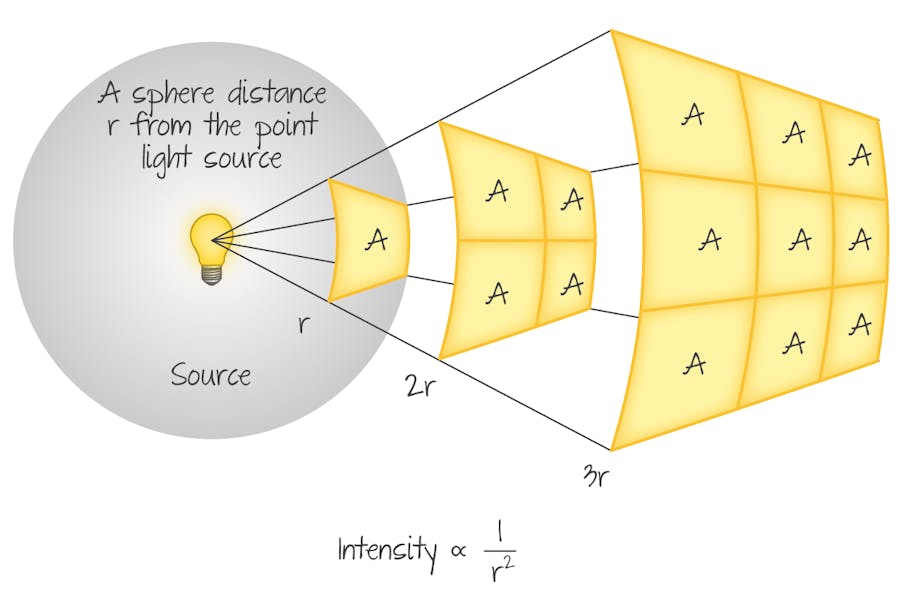
The answer is intensity. Intensity is a measurement of how much energy is being transferred at a unit area, per unit time. If you were, to sum up, all the intensities at every unit area on the wave, that sum would remain constant, no matter how far the wave travelled from its the source.
Intensity is a fairly intuitive concept. As the total energy of a wave covers a larger area, the energy of that wave becomes more dispersed, but the net energy doesn't change. What changes with distance from the source is the intensity of the wave. This is the reason why a torch shined at our eyes from a meter away may temporarily blind us, but a lighthouse beacon 5 kilometres away will not. Even though the total energy of the light beam from the lighthouse is much stronger, the intensity is much lower, as the energy from the beacon is dispersed over a huge area.
Intensity is directly proportional to the total energy.
\(I \propto E\)
Since intensity is inversely proportional to area, it is also inversely proportional to the radius from the source, squared (in most cases, with the exception of things like lasers).
\(I \propto x^{-2}\)
Additionally, the intensity is proportional to amplitude squared. There isn't a simple DP way of explaining why, but if you're interested in the derivation, click this link below. Bear in mind that you don't need to know this.
https://www.quora.com/What-is-the-relation-between-amplitude-and-intensity
Also, a simple formula can be created for intensity, based on total energy and the area in which that energy is dispersed over during that point in time.
Superposition of Waves
Superposition is a phenomenon that describes how waves interact with each other. If two waves in a plane, moving in opposite directions from each other "crash" into each other, the amplitude of displacement from equilibrium of the particle will be equal to the vector sum of the displacement of the two initial waves. Frequency and wavelength don't impact the resulting amplitude.

Animation of two waves, the green wave moves to the right while the blue wave moves to the left, the net red wave amplitude at each point is the sum of the amplitudes of the individual waves.
This is called the superposing of waves. The verb "superpose" means to place one thing on top of another, and in this case, it's the vector displacements that are being placed on top of each other to find the new vector displacement. If two waves are superposed onto each other, this results in what's called interference. Interference is only momentary, and as the waves leave their intersection points and move off, it becomes impossible to tell interference every happened.
Constructive & Destructive Interference
There are two types of interference, constructive interference, and destructive interference.

Constructive interference
Constructive interference (shown on the left) occurs when the vector displacements act in the same direction from equilibrium. This leads to the amplitude to be higher. If the interference is perfectly constructive, then the resulting displacement will be equal to both amplitudes added together.
Destructive interference
Destructive interference (shown on the right) occurs when the vector displacements act in opposite directions from equilibrium. This means that the amplitude of the resulting wave is less than the amplitude of the normal wave. Perfectly destructive interference occurs when the sum of the vector displacements is equal to zero (e.g. equal and opposite wave)
Nodal & Anti-Nodal lines
.0a7adb8d07d2a8fc730e.png?w=900&auto=compress)
Definitions
A nodal line is a set of points where waves interfere destructively and that remain at rest in the equilibrium position while other parts of the medium are in a state of vibration.
An anti-nodal line is a set of points where waves interfere constructively and that have maximum displacements in the medium.
The path (length) difference from two in-phase point sources \(S_1\) and \(S_2\) determines how the two waves superpose at any point.
Calculations
For two in-phase point sources \(S_1\) and \(S_2\), the path difference to points on:
- anti-nodal lines where constructive interference occurs is \(nλ\).
- nodal lines where destructive interference occurs is \((n+0.5)λ\).
In both cases, \(n\) is an integer. When the path difference is zero, this corresponds to the central anti-nodal line.
Double Slit Experiment

Bright fringe positions on a distant screen are equally spaced at separation \(s\) where \(s=\frac{λD}{d}\) where \(D\) is the distance from slits to screen, \(d\) is the slit separation, and \(λ\) is the wavelength. (You will not be examined on this derivation, but you are expected to know and apply it)
Dark fringe positions on the distant screen are equally spaced at the same separation /(s/), centred between the bright fringes. There is a central bright fringe on the screen where the perpendicular bisector of the line joining the double slits meets it.
The Polarisation of Waves
We have seen that electromagnetic waves are transverse, are composed of coupled oscillating electric and magnetic fields that are perpendicular to one another, that the fields can exist and propagate in a vacuum, and that they travel at the universal and constant speed of light, \(, \(≈3.00×10^8m⋅s^{−1}\) in a vacuum and slightly lower in transparent materials.

An electromagnetic wave is linearly polarised if its electric field vector remains in a fixed plane (called the plane of vibration) that contains the direction of wave propagation.
Polarisation is the process by which an electromagnetic wave is polarised.
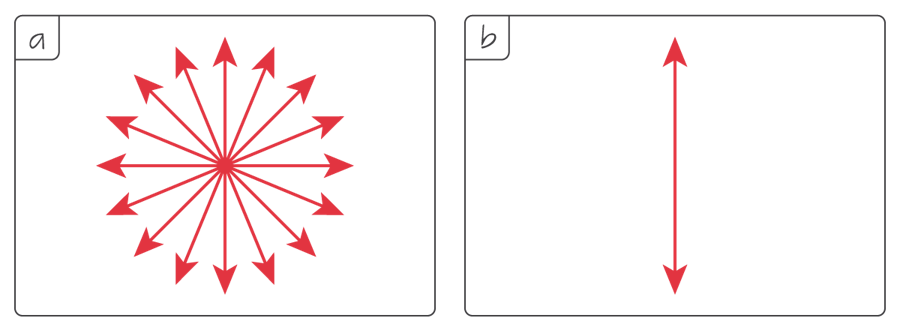
Electric field oscillation directions in an (a) unpolarised and (b) polarised light beam from a viewpoint set in front of it.
By convention, electric field oscillations are used to characterise and illustrate polarised light; perpendicular magnetic oscillations are assumed, but not shown.
Malus' Law
Basically the intensity of light that passes through two polarizing filters is \(=I_0 cos^2\theta\) (found in your formula booklet)
Unpolarised light of intensity \(I_0\) passes through a polariser and then through an analyser whose axis is rotated \(30^ \circ\) from that of the polariser. Determine the intensity of the light between polariser and analyser and the intensity of the light exiting the analyser in terms of \(I_0\).
The initial intensity is \(I_0\).
After passing through the polariser, by extension of Malus' law, the intensity becomes \(I_P = \dfrac{I_0}{2}\).
After passing through the analyser rotated by an angle \(\theta = 30^{\circ}\), by Malus' law, the intensity becomes:
\(I_{A} = I_{P} \cos^2{\theta} \\ = I_{P} \cos^{2}30^{\circ} \\ = \dfrac{I_{0}}{2} \times \dfrac{3}{4} \\ = \dfrac{3 I_{0}}{8}\).
Wave Behaviour
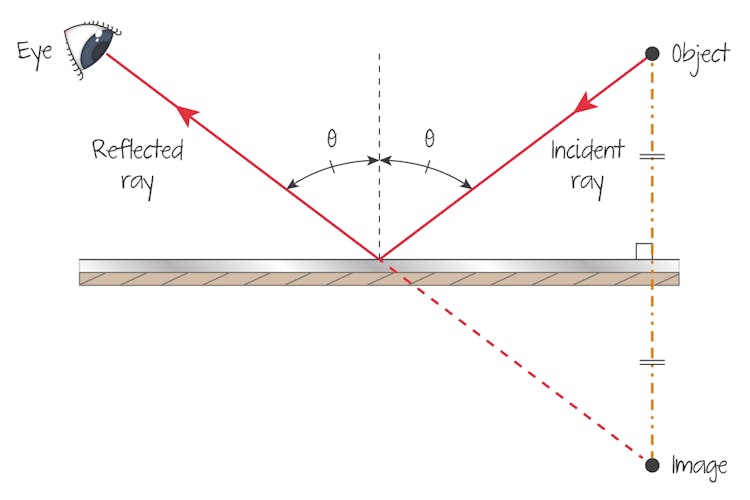
Reflection
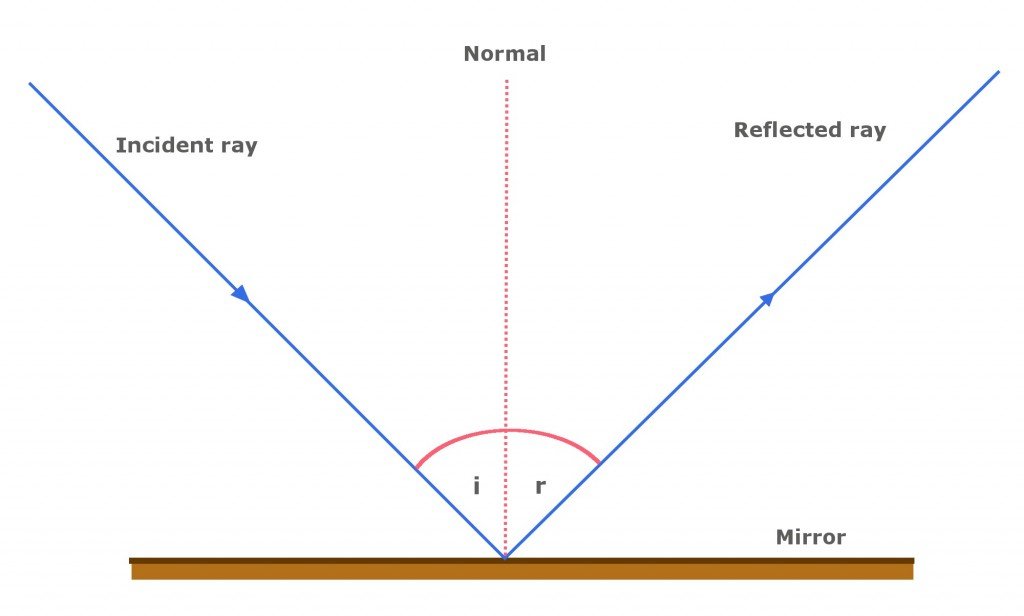
The normal is a line segment that is perpendicular to the surface at the arrival point of the incident ray.
Angles of incidence \((i)\) and reflection are measured between the rays and the normal and all lie in the same plane.
The law of reflection states that for a smooth plane reflector all rays obey: the angle of reflection \((r)\) equals the angle of incidence.
Do not assume that ray angles are always \(45^{\circ}\)!
Refraction
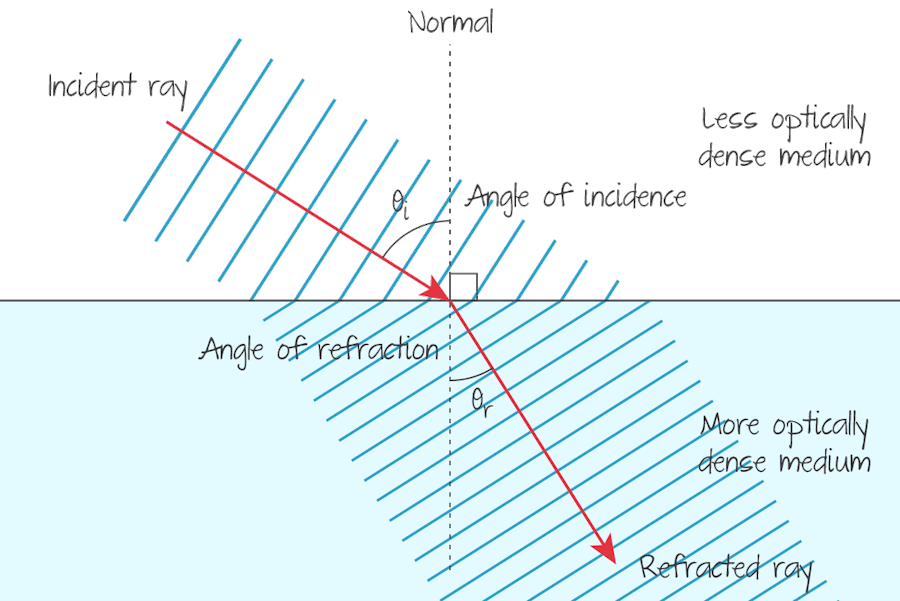
When a ray travels from a less optically dense medium to an optically denser medium, the ray bends toward the normal.
You must add ray arrows and labels to ray diagrams to distinguish between the incident and refracted rays.
Angles of incidence and refraction are measured between the ray and the normal.
Refraction is a change in the direction of a ray that results from a change in the optical density (and wave speed) of the medium it is travelling through.
Refractive Index
The absolute refractive index, n, of a medium is:
\(n = \dfrac{ \mathrm{speed ~of~ light~ in~ a~ vacuum}} { \mathrm{speed~ of~ light~ in~ the~ medium} }\)
Snell's Law
In the Kahn Academy video, they define it as \( \dfrac {v_2} {sin\theta_2} = \dfrac {v_1} {sin\theta_1} \)
But this can also be extended to the formula we have in the Formula Booklet:
\(\dfrac{n_1}{n_2}= \dfrac{\sin \theta_2 }{ \sin \theta_1} = \dfrac{v_2}{v_1}\)
Total Internal Reflection
Total internal reflection is the name given to the full reflection that occurs when a wave travelling in an optically dense medium 1 strikes the boundary of a less optically dense medium 2 at an angle of incidence that exceeds the critical angle.
The critical angle, \(\theta_{critical}\) is defined by \(\sin{\theta_{critical} } = \dfrac {n_2}{n_1}\), where \({n_2},~{n_1}\) are the indices of refraction for the media.

Standing Waves
A standing wave (or stationary wave) is a wave in a medium in which each point on the wave axis has an associated constant amplitude – all points move coherently – and there is no transport of energy. The locations of zero amplitude are called nodes, and the locations of maximum amplitude are called anti-nodes. Adjacent nodes are separated by \(\dfrac {\lambda}{2}\), where \(\lambda\) is the wavelength.
Standing waves are normally produced in a finite (limited and confined) medium with boundaries for reflections that create interference. The boundary conditions – type (free or fixed) and distance between them – can vary. Standing waves fit the boundary conditions (as nodes or anti-nodes) and have wavelengths determined by the wave speed and the associated discrete natural frequencies.
Resonance is the situation in which an external driver oscillating at a system's natural frequency transfers energy into the system, which in this case is the standing wave.
| Wave characteristic | Traveling wave | Standing wave |
|---|
| Wave speed | Determined by the medium. | Zero for a standing wave. |
|---|
| Wavelength | Consistent with \(c = f \lambda \). | Fits finite medium (length) boundaries, fixed or free; consistent with \(c = f \lambda \). |
|---|
| Frequency | Provided by driver oscillator coupled to the medium. | Provided by driver oscillator coupled to the medium, but only discrete frequencies (determined by wavelength boundary fit) can resonate. |
|---|
| Amplitude | Identical for all particles. | Varies from zero to a maximum depending on the particle location in the wave and remains constant (if no energy is added or removed); node spacing is half the wavelength. |
|---|
| Phase | Different for all particles within a wavelength. | Coherent; in-phase within adjacent nodes or anti-phase across adjacent nodes. |
|---|
| Energy | Provided by driver oscillator and transmitted continuously from one location to another. | Provided by driver oscillator at the resonant frequency and not transmitted but rather distributed between nodes, added to and contained in the standing wave. |
|---|
Standing waves on a stretched string of length \(L\) between fixed ends can only occur when \( \lambda_n = \dfrac{2L}{n}~;~n = \{1, 2, 3, \ldots \}\), where the wavelength is \(\lambda\).
The natural frequencies of standing waves on a stretched string of length \(L\) between fixed ends are \(f_n = n f_1~;~n = \{1, 2, 3, \ldots \}\), where \(f_1 = \dfrac {c} {2L}\), and \(c\) is the speed of the travelling wave.
| Harmonic | Pattern | Length-Wavelength Relationship |
|---|
| 1st | | \(\lambda = 2 L\) |
| 2nd | | \(\lambda = L\) |
| 3rd | | \(\lambda = \dfrac{2 } { 3} L\) |
| 4th | | \(\lambda = \dfrac{1 } { 2} L\) |
| nth | -- -- | \(\lambda = \dfrac{2 } { n} L\) |
You are not expected to derive the conditions for standing waves on a stretched string fixed at both ends, but you must know and be able to apply \(\lambda_n = \dfrac{2L}{n}~;~n = \{1, 2, 3, \ldots \}\), where wavelength is \(\lambda\) and \(f_n = n \dfrac {c} {2L}~;~n = \{1, 2, 3, \ldots \}\), where frequency is \(f\) and the definition of harmonics. You must also be able to sketch and interpret standing waves according to their boundary conditions and to identify and use harmonics, determine wavelengths, frequencies, and wave speed for resonance conditions.
Editors- EightTrigrams - 2163 words.
- joeClinton - 3 words.
- CD_FER - 2134 words.
View count: 17604