Old Vector Notes

A vector is a mathematical quantity that has both a magnitude and a direction. In maths, vectors are an expression in terms of there perpendicular components. In two dimensions, they are represented as

$\left(\begin{array}{c}x\\ y\end{array}\right)$

The magnitude of a vector denoted with the absolute value symbol. 

$\left|a\right|$

This magnitude can be calculated using Pythagoras's theorem. 

$\left|a\right|=x^2+y^2$

It is the sum of the perpendicular components squared. 

In maths, a vector is defined only by it's magnitude and direction. If two vectors have the same magnitudes and are parallel, then they are the same, even if they are in different positions. 

Adding and subtracting vectors

To add vectors algebraically, you have to add the perpendicular components of each vector to each other. This always created a third vector

$\left(\begin{array}{c}a\\ c\end{array}\right)+\left(\begin{array}{c}b\\ d\end{array}\right)=\left(\begin{array}{c}a+b\\ c+d\end{array}\right)$

Graphically, this means placing the tail of the second vector onto the head of the first vector. The resultant vector goes from the tail of the first vector to the head of the second vector. 

Prior Knowledge

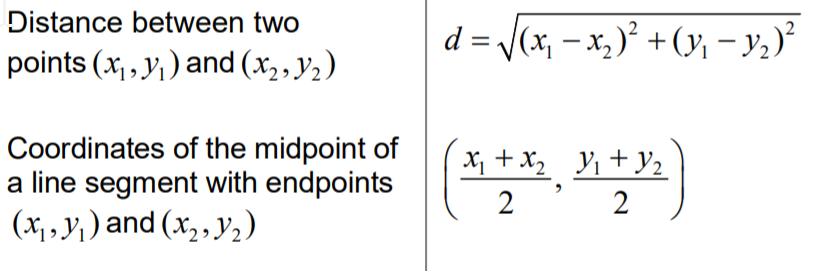
The formula you should be comfortable using:

Vectors

→AB ≠ →$\stackrel{}{\mathrm{B}\mathrm{A}}$  as the starting and end points are different.

View count: 2593