Warning: these notes are a work in progress and are not finished yet. You can help to finish this page by signing up and clicking edit at the top of the page.

What is a Function?

A function is a special relationship where each input has a single output. It is often written as $f(x)$ where $x$ is the input value. Example: $f(x) = \frac{x}{2}$ ("f of x equals x divided by 2"). It is a function because each input $x$ has a single output.

Vertical Line test

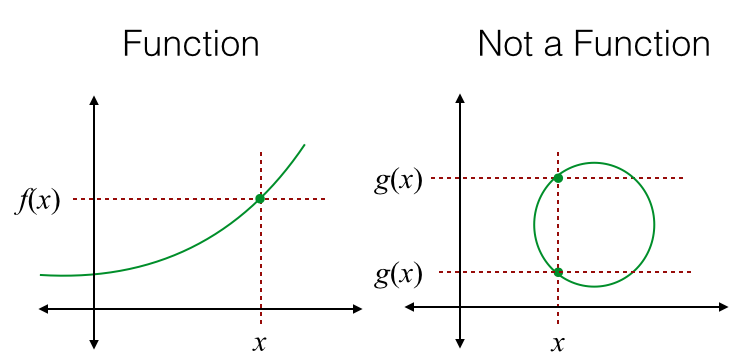
Image result for vertical line test for functions diagram

A test that can be used to determine if a relation is a function. A relation is a function if there are no vertical lines that intersect the graph at more than one point. Note that all functions are relationships, but not all relationships are functions.

Domain and Range

If you are comfortable with domain and Range already in forms like Domain X ∈ [1,5] or 1 ≤ X ≤ 5, Range Y ∈ ]2,10[ or 2 < X < 5 Then you can move on.

If you have any issues this might help:

\iframe{https://www.youtube.com/embed/96uHMcHWD2E}

\iframe{https://www.youtube.com/embed /-DTMakGDZAw}

Composite Functions

The composition of two functions $f(x)$ and $g(x)$ such that function g(x) is applied first and function $f (x)$ is applied second is the function $f \circ g (x)$ . It maps x to $f (g (x))$ and we write:

$(f \circ g) (x) = f (g (x))$

Be careful to read composite functions in the correct order, read from right to left. The function closest to the x is the first function to be executed, the result of which is given to the next.

The domain of composite functions

The domain of the function f∘g is the set of all possible x values of g such that the respective g(x) belongs to the domain of f.

Inverse functions

Now let us consider the function $f (x) = 2 x$ .

$f^{- 1} (x)$ undoes the action of f(x) and therefore $f^{- 1} (x) = x / 2 .$

It is enormously important that you do not think of it as "one over f". Note that $\frac{1}{f (x)}$ is written as $[f (x)^{- 1}]$

On a graph, $f (x)$ and $f^{- 1}$ are symmetric in the line y = x, meaning that if you reflect $f (x)$ in y=x then you obtain $f^{- 1}$ , and vice versa.

Finding the inverse of functions ( $f^{- 1} (x)$ )

Write $y = f (x)$ .
Then replace all the x's with y's, and the y's by x's.
Solve until you obtain an expression $y = g (x)$ , where $g (x)$ includes all components except y.

The Reciprocal function

The reciprocal function of f(x) is the function that maps any x value (except x≠0) to

\frac{1}{x}

and thus,

f (x) = \frac{1}{x}

Remember the reciprocal function and any multiple is self-inverse (the inverse is the same as the original).

Transformations of Functions and Graphs

There are 3 types of transformations:

Translations

Variable	function	result	notes
$h$	$y=f(x-h)$	Translating the graph towards the right/left	Right when $h$ is positive
$v$	$y=f(x)+v$	Translating the graph upwards/downwards	Upwards when $v$ is positive

\graph{{x^2+1},{(x-1)^2}}

Scalings

Variable	function	result	notes
$s$	$y=s(f(x))$	Stretching/compressing the graph along the y-axis	Stretching when s > 1
$c$	$y=f(cx)$	Compressing/stretching the graph along the x-axis	Compressing when c > 1

\graph{{1.5x^2},{0.2x^2}}

Reflections

function	result
$y = - f (x)$	Reflection across y-axis
$y = f (- x)$	Reflection across x-axis

\graph{{y=x}}

Review

Type of Transformation	Equation
Vertical Translation	$y=f(x)+v$
Horizontal Translation	$y=f(x-h)$
Vertical Stretch	$y=sf(x)$
Horizontal Stretch	$y=f(cx)$
Vertical Reflection	$y=-f(x)$
Horizontal Reflection	$y=f(-x)$

It is also worth noting that more than one transformation can occur. For example, the function $y=2x^2+3$ can be viewed as the basic quadratic function $y=x^2$ stretched vertically by a factor of 2 and shifted vertically by a factor of 3.

\graph{{4x^2+2}}

Editors

CD_FER - 805 words.
joeClinton - 71 words.

View count: 3443

Functions