Rigid bodies and rotational dynamics
So far, you've probably only considered the effect a force has on linear motion. However, as I'm sure your intuition tells you, a force can also make an object rotate. For example, the flicking motion of the wrist when a frisbee is thrown, which gives the frisbee an angular acceleration. Or when a football is kicked, and it spins.
The Centre of Mass

The centre of mass of an object is the point on the object from which there is an equal amount of mass in every direction. When a force is applied directly to the centre of mass, only linear acceleration can occur. The centre of mass can be computed with an integral, or with a summation, but it's not necessary to know it for the IB. The centre of mass doesn't necessarily have to be on the object. For example, will a hollow ring, the centre of mass will always be in the centre.
Rotational Equivalents of Linear Motion
The laws describing rotational motion are very similar to the laws describing linear motion. Most of the mathematical quantities used to describe linear motion have rotational equivalents.
| Linear Equivalent | Rotational Equivalent | Description of the rotational equivalent |
| Displacement | Angular displacement | The change in angle. One revolution is 2pi radians or 360 degrees. Represented with the symbol theta, and measured in radians. |
| Velocity | Angular velocity | The derivative of angular displacement with respect to time. or when it's constant Measured in radians per second. Rads*s-1 |
| Acceleration | Angular acceleration | The second derivative of angular displacement with respect to time, and the first derivative of angular velocity with respect to time. Measured in radians per second squared. Rads*s-2
|
| Force | Torque | The "turning effect" of a force applied to an object. The larger the torque, the larger the change in angular acceleration. Torque is the cross product of the force vector and the displacement from the centre of mass. This is intuitive because if the force acts straight on the centre of mass, only linear acceleration will occur. . Theta is obviously the angle between the two vectors. There is also a rotational equivalent of Newton's second law (F=ma). The net torque can also be calculated in a similar way. It is the product of the momentum of inertia and the angular acceleration. |
| Mass | Moment of Inertia | The resistance to angular acceleration due to torque. The larger the moment of inertia of an object, the less angular acceleration produced by a given torque. It is due to the distribution of mass, and it depends on the shape and density of an object. It is calculated as the sum of the product of the mass of every particle, and the distance from the particle to the axis of rotation. |
| Momentum | Angular momentum | The angular momentum of a system always remains constant, unless a net torque is acting on the system. Because it is a conserved quantity, it's incredibly useful. Angular momentum is calculated as the product of the momentum of inertia, and the angular velocity of rotation. |
Torque
Torque is the ability of a force to rotate an object. It is equal to the product of the magnitude of the force and the perpendicular distance between the axis of rotation and the line of action of the force (known as the lever arm or moment arm).
Remember to set your calculator to Deg
\(\Gamma=Fr\sin\theta\)
Couples
A couple is a pair of parallel forces of equal magnitude but with different lines of action and acting in opposite directions.

Equilibrium
Translational equilibrium occurs when the resultant force on an object is zero.
Rotational equilibrium occurs when the resultant torque on an object is zero.
Remember that \(F = m \times a \)
When considering an object in rotational equilibrium, it is necessary to calculate the resultant torque with respect to a certain point. Any point can be chosen, not just the axis of rotation. To simplify your calculation, choose a point where the torque of as many of the forces you do not know or need to find out is zero. That is, choose a point through which the lines of action of these forces pass.
Two children sit on a 1.5 m long seesaw, which is pivoted at its center. The younger child, whose mass is 25 kg, sits at the furthest point on one side of the seesaw. The older child, whose mass is 41 kg, sits on the other side, ensuring that the seesaw balances. How close to the pivot is the older child?
0.46 m (2s.f.)
Moment of Inertia and Conservation of Angular Momentum
The Moment of inertia of an object defined as the sum of this expression below for every single particle.
\({m_p r_p}^2\)
mp represents the mass of the particle, and rp represents the distance of the particle from the axis of rotation.
This expression tells us a lot about the moment of inertia of a rotating object.
Firstly, the axis you rotate it around matters. This is because the rp2 value will change for most particles when the axis of rotation is changed.
Secondly, if the mass is distributed further from the axis of rotation, the object becomes harder to rotate, as it has a larger moment of inertia. This is why divers bring their legs in when they do front flips.
Thirdly, if the mass is larger, the object becomes harder to rotate.
The fourth thing is when you want to find the moment of inertia of a complicated shape, you can break it down into simple shapes, and add their moments of inertia about the axis of rotation.
The moment of inertia \((I)\) can be calculated from the sum of the mass of all of the particles of which the object is comprised \((m)\) multiplied by the square of their distance to the axis of rotation \((r)\):
\(I=\displaystyle\sum m r^2 \)
For a composite object, calculate the value of \(mr^2\) for each component, then add them together.
Four equal masses of ${m}00 g are attached by light, rigid rods to form a square of side ${l}0 cm. The square rotates around its center. What is its moment of inertia?
=(4*${m}/10*${l}/10*SQRT(2)/2) & " kg m^2"
Practice Exam Question [question]
A constant force of 50.0 N is applied tangentially to the outer edge of a merry-go-round. The following diagram shows the view from above.
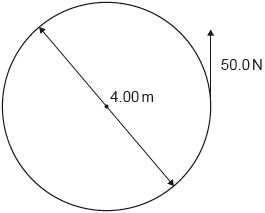
The merry-go-round has a moment of inertia of 450 kg m2 about a vertical axis. The merry-go-round has a diameter of 4.00 m.
The merry-go-round starts from rest and the force is applied for one complete revolution.
A child of mass 30.0 kg is now placed onto the edge of the merry-go-round. No external torque acts on the system.
The child now moves towards the center.
What is the angular acceleration of the merry-go-round?
\( \Gamma = Fr = 50 \times 2 = 100 Nm \)
\(α = \frac{\Gamma }{I} = \frac{{100}}{{450}} =0.22 rads^{–2}\)
Final value to at least 2 sig figs, OR clear working with substitution required for the mark.
[2 marks]
Calculate, for the merry-go-round after one revolution, the angular speed, and the angular momentum.
\(\omega _t^2 - \omega _0^2 = 2\alpha \Delta \theta\)
\(\omega _t^2 - 0 = 2 \times 0.22 \times 2\pi\)
\({\omega _t} = 1.7 rads^{-1}\)
Accept BCA, values in the range: 1.57 to 1.70.
[1 mark]
\(L = Iω = 450 x 1.66\)
\(= 750 kgm^2 rads^{-1}\)
Accept BCA, values in the range: 710 to 780.
[1 mark]
Calculate the new angular speed of the rotating system and state why the angular speed will increase.
\(I = 450 + mr^2\)
\(I = 450 + 30 × 2^2 = 570 kgm^2\)
\(L = 570 × ω = 747\)
\(ω = 1.3 rads^{-1}\)
Watch for ECF from (a) and (b).
Accept BCA, values in the range: 1.25 to 1.35.
[2 marks]
angular momentum will be constant «as the system is isolated»
«so the angular speed will increase»
[2 marks]
Calculate the work done by the child in moving from the edge to the center.
\(W = ΔE_k\)
\(W = \frac{1}{2} × 450 × 1.66^2 – \frac{1}{2} × 570 × 1.31^2 = 131 J\)
Accept BCA, the value depends on the answers in previous questions.
[2 marks]
Rolling Without Slipping
When an object rolls without slipping, the instantaneous linear velocity at the point of contact with the surface is zero. This occurs when \(v=ωr\).
Rolling without slipping means that the point of contact between the wheel and the floor is instantaneously at rest.
A body that is rolling without slipping is moving in both a translational and rotational motion (because it’s rotating, it is rotational motion, and because it is moving forward and not staying in the same place, it is translational motion as well). Every point on the body has the same angular velocity ω, and the same linear speed v = ωR. If that body was moving forward without rotating every point on it would have a velocity u to the right. If the wheel is sliding, however, every point has 2 motions, and, therefore, 2 velocity components: due to rotating and due to sliding.
Top point: v = ωR + u. Bottom point: v = ωR - u, but since this point is instantaneously at rest v = 0 and u = ωR. Therefore, we can rewrite:
Top point: vt = 2ωR m/s
Centre of mass: vcm = ωR m/s (it is not rotating, so the velocity is only due to the translational motion)
Bottom point: vb = 0 m/s
Because angular acceleration is the rate of change of angular velocity, the condition of rolling without slipping may be expressed in terms of angular acceleration as a = αR.
Thermodynamics
The first law of thermodynamics
The first law of thermodynamics: The total energy of an isolated system is constant, energy can be transferred from one form to another but not destroyed. (law of conservation of energy)
This law means that when energy is applied to a system it is either converted to internal energy or to thermodynamic work, but is never lost. This gives the following important formula:
\(Q= \Delta U + W \)
Calculating internal energy (of an ideal gas)
Internal energy (\(U\)) is given by this formula:
\(U= \frac{3}{2} n \cdot R \cdot T \)
- R = gas constant (8.31, can be found on the data page)
- n = number of moles
- T = temperature
For ideal gases, the internal energy is the same as the total kinetic energy of a substance, since potential energy is assumed to be 0 (discussed in the thermal physics unit). So to derive this formula we take the average kinetic energy formula and multiply by the number of molecules. Then we perform some substitutions to change the variables and simplify.
\(U=\frac{3}{2} K_b T \cdot N = \frac{3}{2} \frac{R}{N_A} T \cdot N \cdot N_A = \frac{3}{2} n R T \)
Calculating thermodynamic work
The other way that heat energy can be transferred is by doing work. This is due to the gas particles bouncing against the walls of their container causing them to expand.
Work (\(W\)) is given by this formula:
\(W = p \Delta V \)
This can be derived by taking the standard formula for work: \(W=Fd\), substituting \(pA\) for F and then simplifying \(A \cdot d \) to \(V\)
\(W = F\cdot d = pV\)
Sign conventions
| Sign | \(Q\) | \(\Delta U\) | \(W\) |
| Positive | Thermal energy is added to the gas | Increase in internal energy | Work is done by the gas |
| Negative | Thermal energy is removed from the gas | A decrease in internal energy | Work is done on the gas |
Thermodynamic processes
| Process | Definition | Application of 1st law |
| Isothermal | Temperature is constant | Temperature changes internal energy so \(\Delta U=0\) and \(Q=W\) |
| Isovolumetric | Volume is constant | Volume changes require work so, \(W=0\) and \(Q= \Delta U\) |
| Isobaric | Pressure is constant | Even if pressure is constant temperature and volume will still change so \(Q = \Delta U + W \) |
| Adiabatic | No thermal energy is exchanged with the surroundings | Thermal energy is \(Q\), so \(Q=0\), so \(\Delta U = -W \) |
Adiabatic processes for monatomic gases
Note: An adiabatic process must happen quickly and the container must be well insulated, otherwise heat will be lost to surroundings.
A formula which is used to solve adiabatic problems is:
\(pV^{\frac{5}{3}}=\rm{constant}\)
The derivation of this formula is too complicated, so we just use it and don't ask questions.
We can also use \(pV = nRT\) to derive: \(T_1 V_1^{2/3}=T_2 V_2^{2/3}\). This tells us that an adiabatic expansion in volume will cause a decrease in temperature and an adiabatic compression in volume will cause an increase in temperature. You think of it like the volume increasing can't take energy from its surroundings so it takes it from the internal energy.
pV diagrams and thermodynamic cycles
pV diagrams are used to show changes in pressure and volume. Temperature is not shown and has to be imagined to be changing. The only case that the temperature does not change is if the curve is \(P= \frac{1}{V}\) .

- Adiabatic processes are like isothermal except steeper because there is a temperature change.
It is important to stress that although during an adiabatic process there is no thermal energy transfer with the surroundings, the temperature of the gas will change because work has been done.
Calculating work from a pV diagram
If a question asks you to calculate work and pressure is not constant, then you must calculate work graphically with a pV diagram.
Work on a pV diagram is the area below the curve. This is because the area below gives the product of p and V which is work. \(W = pV\)
Thermodynamic cycles
a thermodynamic cycle is a sequence of process which in turn change the pressure, temperature and volume of a gas but eventually return it to its initial state. These cycles do work to either remove energy from the surroundings or add energy
Work done by the thermodynamic cycle: This is equal to the area enclosed by the cycle on a pV diagram.

The second law of thermodynamics
Entropy: This is a measure of the amount of disorder in a system
Calculating entropy
to calculate change in entropy we use this formula:
\( \Delta S = \frac{\Delta Q}{T}\)
- \(\Delta Q\) is the amount of heat transferred to or from a system
- T is the temperature of the system
This formula requires the temperature to be constant
1592951269.png)
A heat engine operates on the cycle shown in the pressure-volume diagram. The cycle consists of an isothermal expansion AB, an isovolumetric change BC, and an adiabatic compression CA.
State and explain at which point in the cycle ABCA the entropy of the gas is the largest.
Entropy is largest at B
entropy increases from A to B because T = constant but volume increases so more disorder or ΔS = Q\T and Q > 0 so ΔS > 0
entropy is constant along CA because it is adiabatic, Q = 0 and so ΔS = 0
OR
entropy decreases along BC since energy has been removed, ΔQ < 0 so ΔS < 0
[3 marks]
Ways of stating the second law
- Plank Statement: In an irreversible process the amount of entropy increases and in a reversible process the amount of entropy stays the same.
- Clausius statement: Thermal energy cannot be spontaneously transferred from a cold body to a hot body.
- Kelvin statement: In a cyclic process it is impossible to fully convert heat into work.
Thermal efficiency and the Carnot cycle

Heat engine: Something which converts heat energy to mechanical energy.
Thermal efficiency
This is the ratio of useful work done to input work in a thermodynamic cycle- This tells us how efficient the cycle is. The efficiency is \( \eta\)
Formula: \(\eta=\rm\dfrac{useful \ work \ done}{energy \ input}\)
We can use the thermal efficiency formula to compare how efficient different heat engines are.
Carnot cycle
This is the most efficient thermodynamic cycle. It has four steps:
- Isothermal expansion
- adiabatic expansion
- Isothermal compression
- Adiabatic compression
Note: All the processes are reversible so the whole cycle is reversible.
The Carnot cycle has two isotherms which are at the temperature of the two heat sources, hot and cold.
Carnot cycle efficiency
\(\eta_{carnot}=1-\dfrac{T_{cold}}{T_{hot}}\) (fortunately this is in the data booklet)
Fluid dynamics (HL)
Density and pressure
Density: The mass in kilograms per meter cubed of volume
Pressure: The force applied to a surface divided by the area it is applied over
Buoyancy and Archimedes principle
The buoyancy force is the force felt by an object partially/completely submerged in a fluid. It is the result of their being a greater force on the bottom of the object than on the top.
Archimedes principle and the equation of buoyancy.
Archimedes principle states that the force experienced on a submerged or partially submerged object due to buoyancy is equal to the weight of the liquid being dispersed by the object.
So to calculate buoyancy we calculate the weight of the dispersed liquid by multiplying the density of the liquid by the volume of the object and then by the acceleration due to gravity. This gives:
\(F_b = \rho V g \)
Pascal's Principle
Pascal's principle states that a change in pressure in one part of an enclosed fluid is transmitted undiminished to all parts of the enclosed fluid and the walls of the container.
This means that pressure is constant everywhere.
\(\frac{F_1}{A_1} = \frac{F_2}{A_2} \)
Amplification of force
This formula also means that if the area at which the pressure is being applied becomes much larger then the force must be amplified to keep pressure constant. To find the ratio of amplification we can rearrange the formula:
\(\frac{F_1}{F_2} = \frac{A_1}{A_2} \)
Hydraulic lift problems
A hydraulic lift is used to lift heavy objects. It is made up of a small piston with a small area connected via reservoir of liquid to a big piston with big area.

This difference in area means that if a force \(F_1\) is applied to the small piston the force is amplified to a larger force
Fluids in motion
Hydrostatic equilibrium
A fluid where the forces acting on it balance, causing it to remain at rest or move at a constant velocity. This is equivalent to translational equilibrium, in mechanics.
Hydrostatic pressure: the pressure that is exerted by a fluid at equilibrium at a given point within the fluid, due to the force of gravity.
The ideal fluid
As real fluids can be complicated to model, physicists look at instead the ideal fluid which simplifies calculations. The idea fluid is based on a number of assumptions:
- Non-viscous: Does not exert forces on other fluids.
- Flows steadily: Fluid velocity of a point in the fluid is constant
- Incompressible: The fluid cannot be compressed and so density is constant throughout
Streamlines
Streamlines are curved lines that show the instantaneous velocities of a of a fluid.
Continuity equation
The continuity equation is:
\(Av = \rm constant \)
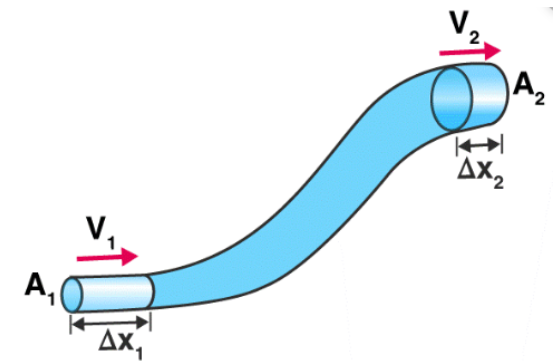
This tells us that if the cross sectional area of the pipe a fluid is flowing through becomes smaller then the velocity will increase proportionally. For example, water coming out of a hose flows faster when you pinch the nozzle reducing the area.
How is the continuity equation derived
Since ideal gases are incompressible. The amount of fluid entering from one side of a pipe per second must be equal to the fluid exiting from the other side per second. We can calculate the volume entering per second by multiplying the area by volume. Therefore since this is volume per second remains constant, \( Av = \rm constant \)
Bernoulli equation
The main idea of the bernoulli's equation is that the sum of static pressure, kinetic energy and potential energy must stay constant no matter how the fluid or its container changes. This, like the continuity equation, is derived from the law of conservation of energy.
Formula
- \rho is density, z is height, v is velocity, P is pressure
- Kinetic energy: \frac{1}{2}\rho v^2
- Grav. Potential energy: \rho gz
- Static pressure: P
Derivation (not required)

Applications of Bernoulli principle
When applying the bernoulli principle, there are two steps:
- Determine which variables will stay constant and simplify the formula accordingly
- Solve for the needed unknown
| Application | Constant variables / assumptions | Solution | Diagram |
Fluid flowing freely from a container (find velocity) | - Pressure is constant as container has constant radius.
- initial velocity = 0
| |  |
Venturi metre (find pressure/height difference) | - Height (inside tube) is constant
| |  |
pitot static tube (find fluid speed) | - Height constant
- Final velocity = 0
| |  |
Airfoil (determine lift) | - Height constant as we assume airfoil is very thin.
| | 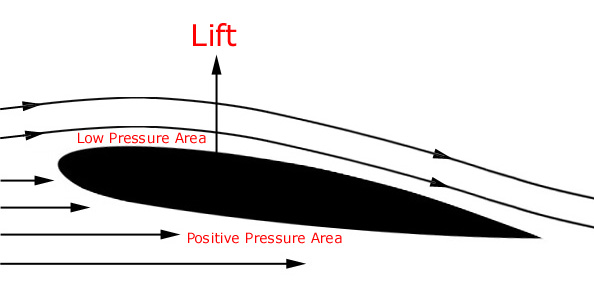 |
Stokes’ law and viscosity
Viscosity
A measure of a fluids resistance to deformation at a given rate.
\( \eta\) is the viscosity of the fluid, with units of pascal seconds \(Pa \dot s \)
Stokes law
Stokes law says that for small spherical objects at low velocities the drag force is proportional to viscosity, radius and velocity.
- \(\eta\) is viscosity
- r is radius of spherical ball
- v is flow velocity
Laminar and turbulent flow and the Reynolds number
Laminar and turbulent flow
Laminar: Flow is regular and streamline do not cross
Turbulent: Flow is irregular and streamlines cross.

Reynold number
Reynolds number: A number which gives an indication of how turbulent a fluid's flow is.
The formula to determine the reynold number is:
\(\displaystyle R = \frac{vr\rho}{\eta} \)
where:
- v is velocity
- r is resistance
- \(\rho\) is density
- \(\eta\) is viscosity
Note: If the Reynolds number is less than \(1\times 10^3\) then the fluid is assumed, by the ib syllabus to be laminar.
Forced vibrations and resonance (HL)
Damping
Damping: when an oscillating object loses energy, due to resistive forces, reducing the amplitude of oscillation.
Degrees of damping

| Damping degree | description | Q-factor | Example |
| Underdamped | A small amount of damping, meaning it will continue to oscillate but the amplitude will decrease exponentially. | Q>0.5 | Spring in water |
| Critically damped | It comes to rest at equilibrium as fast as possible. | Q=0.5 | Shock absorbers in cars |
| Overdamped | There is a large amount of damping, so instead of oscillating it just comes to rest very slowly. | Q<0.5 | Spring in honey |
Q-factor
The Q factor stands for the quality factor and is the degree of damping is given by the Q factor. This is given by the following formula:
- It is a ratio of the peak amount of energy to the energy lost per cycle.
- The larger the q-factor the less damping there is.
- It is approximately equal to the number of cycles an object will oscillate before coming to rest.
Note: Remember that the energy stored in an oscillation system is proportional to the amplitude squared!
The graph below shows the displacement y of an oscillating system as a function of time t.
1592962125.png)
A. State what is meant by damping.
B. Calculate the Q factor for the system.
C. The Q factor of the system increases. State and explain the change to the graph.
A. The loss of energy in an oscillating system [1 mark]
B. \(Q = 2\pi \frac{{{{16}^2}}}{{{{16}^2} - {{10}^2}}} \approx 10\) Accept any answer from 9 to 11. [1 Mark]
C. The amplitude decreases at a slower rate [1] a higher Q factor would mean that less energy is lost per cycle [1] [2 marks total]
Example problems
- A mass on the end of a spring is displaced by 12 cm. After one full oscillation, the amplitude is reduced to 6 cm. What is the value of the Q factor and the degree of damping?
- Energy before = \(\frac{1}{2}\cdot k \cdot 12^2\)
- Energy after = \(\frac{1}{2}\cdot k \cdot 6^2\)
- \(Q = 2\pi \frac{72k}{72k-54k} = 8.4\)
- 8.4>0.5 so the degree of damping is underdamped.
- After approximately how many oscillations will a pendulum come to rest if it dissipates one-fourth of its energy every cycle?
- \(Q = 2\pi \frac{1}{1/4} = 25.133\)
- Q is around 25 so there will be approximately 25 oscillations.
Free and force vibrations
Natural frequency: This is the frequency that an object will oscillate at following a disturbance, in the absence of any driving force or damping force.
Free oscillation: An oscillation that occurs without there being any external forces.
Forced oscillation: A system, which due to the presence of an external periodic stimulus, oscillates at a frequency other than the natural frequency.
Resonance
Resonance is the increase in amplitude in a forced frequency when the driving frequency matches the natural frequency.
For example, if you are swinging on a swing, the motion of your legs, which is in effect a driving frequency will have the most effect on the height you swing when it matches the natural frequency of the swing. Another example is with a wine glass. If you sing at the same frequency as the natural frequency of the glass, it will resonate and eventually vibrate so much it breaks.
The phase relationship between the driving frequency and forced oscillations
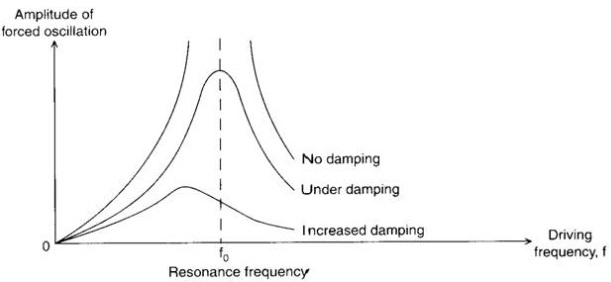
- The closer the driving frequency is to the natural frequency, otherwise known as the resonance frequency, the greater the resonance.
- The damping degree affects what the max amplitude will be
- With no damping, the resonance can keep increasing until the system breaks
- With under damping, there is a high max amplitude.
- At high damping, there will be a low max amplitude, and the maximum driving frequency will be slightly less than the natural frequency.
Useful and destructive effects of resonance
Useful effects:
- Resonance of quartz crystals allows for accurate timing devices.
- Resonance of protons in an MRI scan
- Resonance allows microwaves to make water molecules vibrate and heat up.
Destructive effects:
- Bridges can collapse if wind resonates at the natural frequency of a bridge.
Resonance form of Q-factor
The energy lost per cycle is equal to the power loss divided by the frequency of oscillations
\(Energy dissipated per cycle = \frac{power loss}{resonant frequency}
This gives an alternative form of the Q-factor formula, with power loss and resonant frequency:
The natural frequency of a driven oscillating system is 6 kHz. The frequency of the driver for the system is varied from zero to 20 kHz.
1592972893.png)
A. Draw a graph to show the variation of the amplitude of the oscillation of the system with frequency.
B. The Q factor for the system is reduced significantly. Describe how the graph you drew in (a) changes.
A. general shape as shown [1] peak at 6 kHz [1] graph does not touch the f axis [1] [3 Marks]
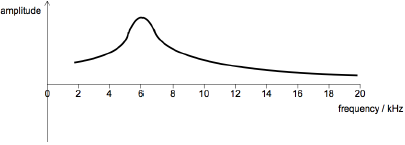
B. peak broadens [1] reduced maximum amplitude/graph shifted down [1] resonant frequency decreases/graph shifted to the left [1] [Max 2 Marks]
Editors- EightTrigrams - 688 words.
- joeClinton - 2540 words.
- CD_FER - 1419 words.
- polina.blinova - 220 words.
View count: 9344