Concept of a limit

The number \(A\) is called the limit of the sequence \(\{a_n\}\) if  \(a_n\) is close to \(A\) for large values of n.

 

The number \(A\) is called the limit (at infinity) of the function f if \(f(x)\) is close to \(A\) for large values of x.

Note that this is closely related to the concept of a horizontal asymptote. If \(A\) is the limit (at infinity) of \(f\), then the line \(y=A\) is a horizontal asymptote of the graph of \(y=f(x)\).

Note that the function does not have to be defined at x=ax=a in order to have a limit. If the function happens to be defined at \(x=a\) and the limit is the same as \(f(a)\) we say that the function is continuous at \(x=a\).

 

The gradient at a point

Differentiation is a way to find the gradient (change in x over the change in y) of a function at any point, written as:

$$ f'(x) \space, \space  y' \space, \space  \frac{dy}{dx} $$

Tangent line to a point on a curve is a linear line with the same gradient as that point on the curve.

 

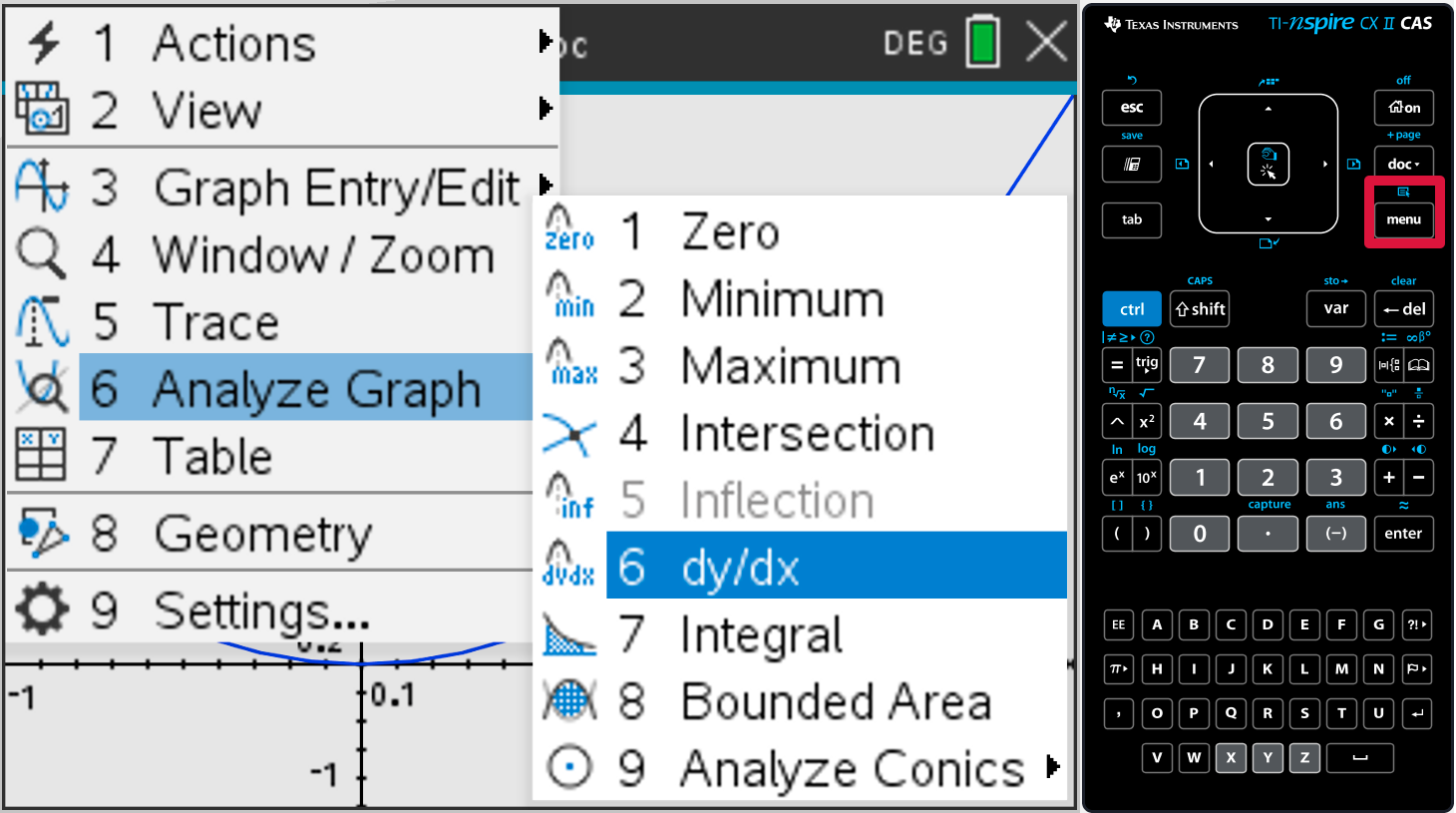
Use your calculator to find the gradient of the graph of \(y=ln(3x2+2)\) at \(x=1\).

 

Gradient function

Common forms of notation for the derivative are \(f'\), \(\dfrac{\mathrm{d}y}{\mathrm{d}x}\)  and \(\dfrac{\mathrm{d}}{\mathrm{d}x}f\). 

 

The diagram below shows the graph of the function f.

 

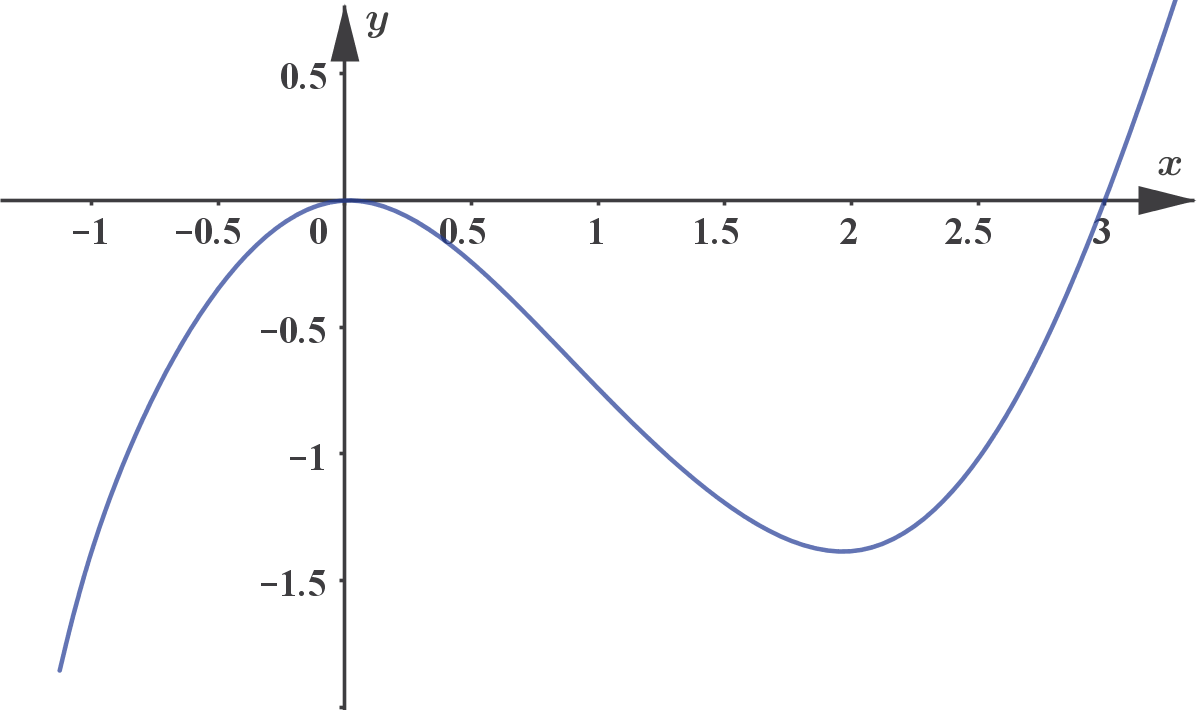
Given that \(f'(a)=−1\), \(f'(b)=0\) and \(f'(c)=3\).

Find the value of a, of b, and of c.

 

Ans: \(a=1\), \(b=2\), \(c=−1\)

 

Graphing the Derivative

Applications

Kinematics

Displacement (s), Velocity (v), Acceleration (a)

 

Graph properties

 

The power rule

If \(f(x)=x^n\), then \(f′(x)=nx^{n−1}\)

This rule is in the formula booklet.

 

The constant factor rule

 If \(f(x)=ax^n\), then \(f'(x)=nax^{n−1}\).

This is not in the formula booklet. You need to remember this rule and, more importantly, make sure that you know how to use it.

 

The sum rule

If \(h(x)=f(x)+g(x)\), then \(h'(x)=f'(x)+g'(x)\).

This is not in the formula booklet. You need to remember this rule and, more importantly, make sure that you know how to use it.

 

The normal

\(M_Normal = - \frac{1}{M_Tangent}

The line that is perpendicular to the tangent to a curve at the point of tangency is called the normal.

Tangent - line with the same gradient as a point on a curve.

Normal - perpendicular to the tangent at a point

Both are linear lines with the general formula: $y = mx + c$.

Finding the Normal

1. Use the derivative to find the gradient of the tangent. For normal
   then do $$ m = \frac{−1}{slope \space of \space tangent}$$
2. Input the x-value of the point into f (x) to find y.
3. Input y, m and the x-value into $y = mx + c$ to find c.

 

The area under a curve

The formula booklet gives the following: 

The area between a curve \(y=f(x)\) and the x-axis, where \(f(x)>0\) is

                \(A = \displaystyle{\int_a^b y\,\mathrm{d}x.}\)

 

Graphical Solve

 

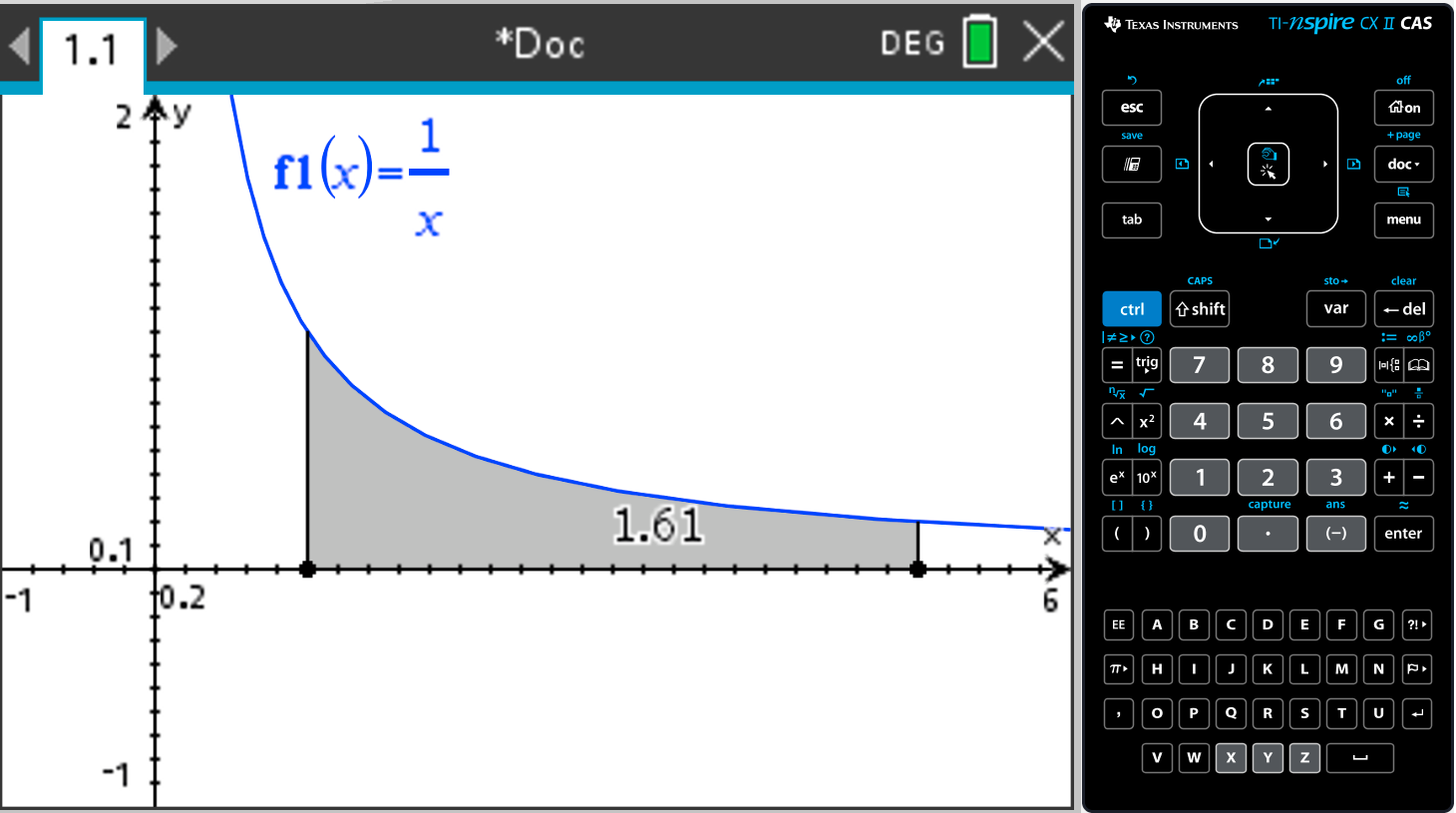
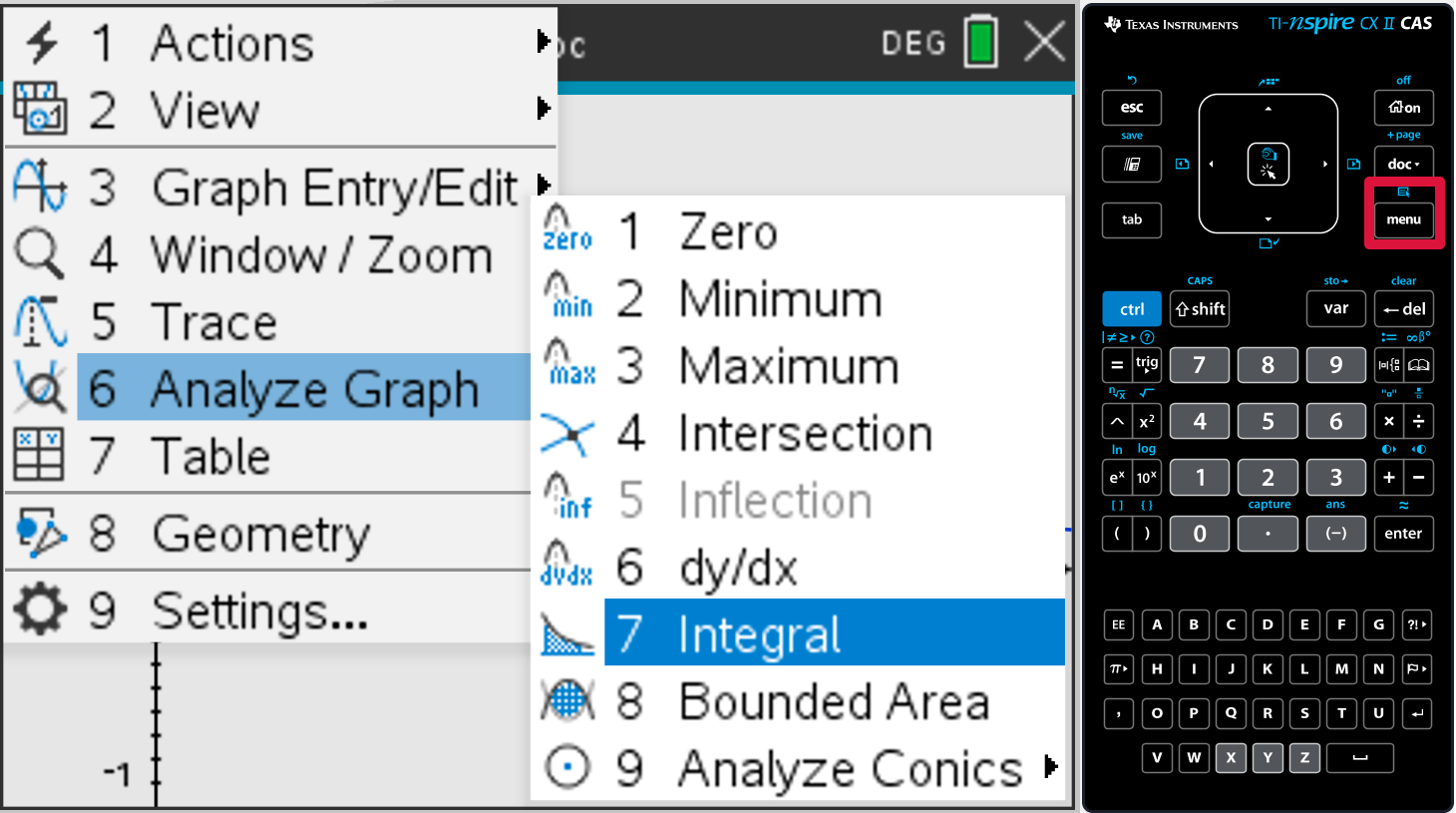
Numerical Solve

 

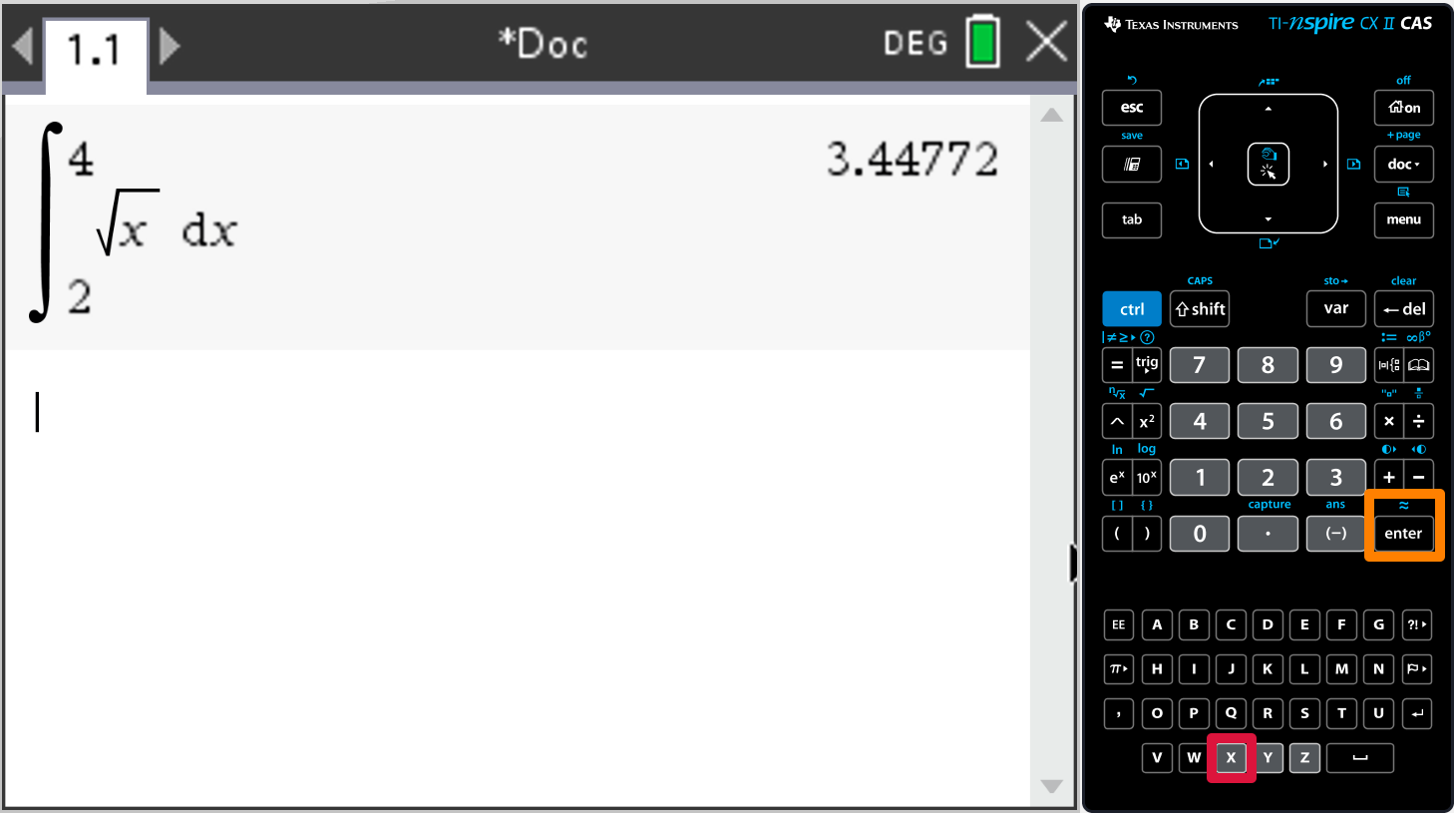
Further differentiation

Exponential Function

If \(f(x)=k\mathrm{e}^{ax+b}\), then the derivative is \(f'(x)=ka\mathrm{e}^{ax+b}​\)​​​​​.

 

Product Rule

Product Rule  $y = uv$, then: $$y' = uv' + u'v$$ 

 

Chain Rule

Chain Rule $y = g (u)$ where $u = f (x)$, then: $$\frac{dy}{dx} = \frac{dy}{du} \times \frac {du}{dx}$$ 

 

Turning points

Point	$f(x)=$	$f'(x)=$	$f''(x)$
Local Min		0	Positive Number
Local Max		0	Negative Number
Point of Inflection			0
Colour	Green	Orange	Red

\graph{{-0.1x^{3}+3x:green},{-0.3x^{2}+3:orange},{-0.6x:red},{x=-3.162:black:dashed},{x=3.162:black:dashed}}

 

 

Sketching Graphs

Gather information before sketching:

Intercepts:

• x-intercept: $f(x) = 0$
• y-intercept: $f(0)$

Turning points:

• Minima: $f'(x)=0$ and $f\text{'}\text{'}\left(x\right)<0$
• Maxima: $f\text{'}\left(x\right)=0$ and $f\text{'}\text{'}\left(x\right)>0$
• Point of inflection: $f\text{'}\text{'}\left(x\right)=0$

Asymptotes

• Vertical: x-value when the function divides by 0
• Horizontal: y-value when x → ∞

Plug the found x-values into f (x) to determine the y-values.

 

 

 

 

View count: 4043