What is an algebraic expression

An algebraic expression describes an amount of something using operators, variables and numbers. 

E.g $\frac{5x}{2}+4$

This in words translates to "5 times the variable x, divided by 2 and add 4".

As a variable is being used this expression can represent an infinite number of values. 

Subsitution  and evaluation

Subsitution

Subsitution is where values are given for certain variables and then all variables in a expression must be replaced with the corresponding variables.

For example if x = 4 and y= 5 then, 

the expression 3x + 2y becomes $3\times \left(4\right)+2\times \left(5\right)$

Evaluation

After subsituting the variables the expression no longer represents infinted values but is instead one finite value and as such can be "evaluating". This simply means: find out what number the expression equals. 

Using basic arthimetic operators. The previous expression, can be evaluated. 

$3\times \left(4\right) + 2 \times \left(5\right) = 12 +10 = 22$

So the evaluated expression is 22.

Simplifiying algebraic expressions

 

Combining like terms

To combine like terms take all terms with the same combination of variables and add them together

E.g $6x^2+8x+9x+12 = 6x^2+17x+12$

In the above example x² cannot combine with 8x as the variable part of the terms do not match. However 8x and 9x can combine to make 17x because the variable parts are both "x", so they match.

Expansion

Expanding single brackets

Algebraic expressions can sometimes have brackets.

E.g $3x·(4+x)$

Inorder to expand the brackets multiply the term on the outside of the bracket, one by one, by the terms inside the bracket.

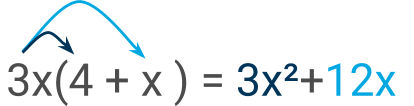
Expanding double brackets

Algebra expressions can sometimes consist of two brackets multiplied together. 

E.g $\left(2x+3\right)·(3x+4)$

Inorder to expand both brackets we need to multiply every term in the left bracket 

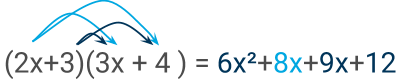
Factorizing a linear expression

This is basically the opposite of single bracket expansion.  

To factorize an algebraic expression: 

1. Find a common factor of all the  terms in the expression
2. Two divide each term by that common factor
3. Wrap the new factored expression in brackets
4. Multiply the common factor by the expression in brackets

E.g $12m + 6 = 6(2m+1)$

Note: To learn how to factorize quadratic expressions visit the Quadratics page

Exponent laws

When variables are raised to a power they have an exponent. For example, x² has an exponent of two.  When two terms with exponents have the same base they can be combined using one of the exponent laws. Which exponent law to use depends on the operator. 

List of laws of exponents

By following the rules described above you can easily combine or simplify exponential terms. 

 

View count: 5297