Simple Harmonic motion
Defining equation
displacement, velocity and acceleration
Kinetic and potential energy
Energy transfer
Period of pendulum and mass-spring
Single-slit diffraction
What is single slit diffraction
Diffraction: a wave phenomena that occurs when a wave comes in contact with an obstacle or a slit.
Single slit diffraction describes how a wave passing through a slit is bent upon exiting the slit. When this new curved wave hits a wall, a single-slit diffraction pattern is seen.
The single pattern is described by:
- A bright central maximum intensity
- Other maller maxima on either side (about 20% of maximum intensity)
- Central fringe is twice as wide as other fringes
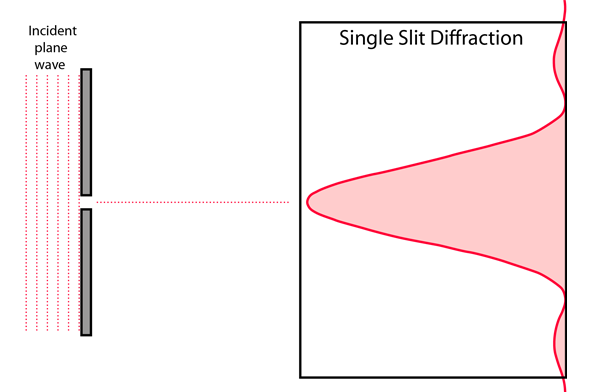
Single slit diffraction pattern explained
The shape and intensity plot of single slit diffraction is caused by an idea known as Huygens' principle. This principle says that at every point on an advancing wave front acts as the center of a new wavelet emanating from that point. Thus we can consider the slit has having a infinite number of secondary wave sources which can constructively and destructively interfere with each other, as shown below.
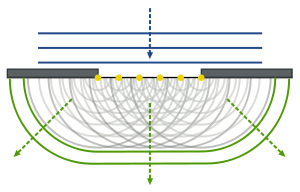
Explanation of central maximum and first minimum
Because the distance between the screen and slit is so big compared to the size of the slit, the angle between a specific point on the screen and any secondary source is approximately equal.
- In the forward direction the angle is zero, which means that as every secondary has the same angle all have the same path difference. This causes constructive interference and there will be a maximum at the center. (This is a bit simplified but the real answer would only confuse you)
- Moving out from the center, there is more and more destructive interference, and the intensity falls
- At a specific point it can be shown that the path difference between a secondary source at the edge and at the center is \(\frac{\lambda}{2}\) and so there is destructive interference resulting in zero intensity. By pairing off every point in the upper half of the slit with on in the lower half, and showing each also has a path difference of \(\frac{\lambda}{2}\), it can proved that at this point there will be an intensity of 0. This is the first minimum.
Single-slit diffraction formula
\(\theta = \frac{\lambda}{b} = \frac{wavelength}{slit diameter}\)
derivation of single slit equation
Since the first minimum is at a point where the path difference between to parallel paths is \(\frac{\lambda}{2}\), we can determine a relationship between the angle from the center, \(\lambda\) and b.
- Using trigonometry we get that \(sin\theta = \frac{lambda}{b}\)
- Since \(\theta\) is very small we can say that \(sin\theta \approx \theta\)
- This gives \(\theta = \frac{lambda}{b}\)
Effect of slit width on single slit diffraction
- From the equation \(\theta = \frac{\lambda}{b}\) we know that as the slit width decreases the angle gets bigger meaning the intensity plot spreads out more
- If the slit is smaller less light is let through and the maximum intensity is less.
Single slit diffraction with white light
White light is a combination of different wavelengths and so when it is incident with a single slit, each wavelength of light will have it's own interference pattern.
- The longer the wavelength the more spread out the interference pattern, the shorter the wavelength the more narrow the interference pattern
- This means when white light passes through a slit it will create rainbow pattern, with the longer wavelengths of light on the outsides and the shorter wavelengths closer to the center.
- The maximum intensity is at the center no matter the wavelength so the first maximum will still be a white fringe.
Young's double slit Interference
Modulation of two-slit interference pattern by one-slit diffraction effect
Multiple slit diffraction
Thin film interference
Resolution
The size of a diffracting aperture
Resolution and Rayleigh criterion
Resolvance of diffraction gratings
Doppler effect
Doppler effect for sound and light waves
Situations involving doppler effect
Determining velocity
View count: 3131