Units

7 Fundamental units

Measurement	Unit	Symbol
Time	Second	s
Displacement	Metre	m
Mass	Kilogram	Kg
Current	Ampere	A
Temperature	Kelvin	K
Amount of substance	Mole	mol
Luminous Intensity	Candela	cd

 

Derived quantities

To convert between the derived and fundamental units, look at the formula and substitute the units. 

E.g Momentum has derived unit - p.

To find fundamental, substitute units into the formula. 

p = mass*velocity = kgms^-1

 

Dimensional consistency

This is checking if the units are correct for measurement by converting it to fundamental units and seeing if it fits the equation. 

E.g are the units for velocity at²?

ms^-1 ≠ ms^-2s²  Therefore this is not dimensionally consistent.

 

Metric multipliers and si prefixes

Factor	Name	Symbol	Factor	Name	Symbol
101	deca	d	10-1	deci	d
102	hecto	h	10-2	centi	c
103	kilo	k	10-3	milli	m
106	mega	M	10-6	micro	μ
109	giga	G	10-9	nano	n
1012	tera	T	10-12	pico	p
1015	peta	P	10-15	femto	f

 

Order of magnitude

The nearest power of 10.

6.5 x 10⁵ has a magnitude of 10⁶ because 6.5 rounds up to 10.

 

Significant figures

Your answer must be to least precise significant figures in the question you were asked.

 

Uncertainties

What is uncertainty

This is how much a value measured may vary from the actual value. 

Absolute uncertainty: the same units as the measurements

percentage uncertainty: Given as a percentage as measurement

 

Precise Vs Accurate

 

Uncertainties Practical

IB Physics: Optional Practical: Density of plasticine

 

Types of error

Type	Description	Effect on the graph
Random	Changes every trial	The best fit line will not pass through all the error bars.
Systematic	Caused by equipment, which is constant for every trial.	Shifts graph vertically or/and horizontally. Error bars represent this error.

 

Rules to determine the uncertainty

Rounding: 1 sig fig on exam OR don't round for lab report

Averages: Range / 2

Analog Measurements: For reliable equipment use plus or minus half smallest division (rounded to 1sf) or the uncertainty listed on the equipment.

 

Combining Uncertainties

Added or subtracted

Add the absolute uncertainty

$\Delta U + \Delta U$

 

Multiplied or divided

Add the percentage uncertainty

$\Delta U\% + \Delta U\%$

 

Raised to a power

Times the percentage uncertainty by the power (X) of the equation

$X \times \Delta U\%$

 

Determine the uncertainty of a series

Calculate the range of values using the min and max value (not the uncertainty).

$\frac{V_{Max} - V_{Min}}{2} = \Delta U$

 

Determine the uncertainty of x number of oscillations

Divide the absolute uncertainty by the number of oscillations.

$\frac{\Delta U}{X}=\Delta U$

 

Trigonometric Uncertainty

Calculate the range of values using the min and max value (normal plus and minus the uncertainty).

$\frac{Cos(V+U)-Cos(V-U)}{2}=\Delta U$

 

Exam Tip

Do not expend a great lot of effort in expressing uncertainties during an examination, unless specifically instructed. Assess the evidence, use common sense, and (generally) round-off absolute uncertainty to one significant figure. An uncertainty of ±0.389s can be rounded to ±0.4s to agree with the least significant digit position in the measured value.

 

Uncertainty graphs

Gradient uncertainty: (Maximum gradient - the minimum gradient)/2

Y-intercept: Maximum/minimum y-intercept - best fit y-intercept (largest difference determines maximum or minimum)

Error bars: Shows the uncertainty of the best line based on the systematic error.

 

Vectors

What are Vectors and Scalars?

A vector is a way of representing a quantity with both magnitude and direction. It can be represented in two ways. Either the magnitude is stated directly,  then it's direction is given as an angle from something. This is useful when working with a polar coordinate system.

Vector: Magnitude and direction

Scalar: ONLY magnitude

 

Examples of vectors and scalars

Vectors	Scalars
velocity	Mass
displacement	Time
Weight	Distance
Acceleration	Length

 

Difficult to remember Vector and scalars quantities

• Electric field strength - Vector
• Current - Scalar
• Work - Scalar

 

Ways of representing a vector

• A plus or minus next to the magnitude
• F = +5N
• An arrow next to the magnitude
• F = 5N ⟶
• A direction next to the magnitude
• F = 5N right
• An angle next to the magnitude (angles always starting from positive x-axis like a unit circle)
• F = 5N 0°

 

Horizontal and Vertical Components

Split each component into its horizontal and vertical components using trigonometry. Then for each axis add the components together. 

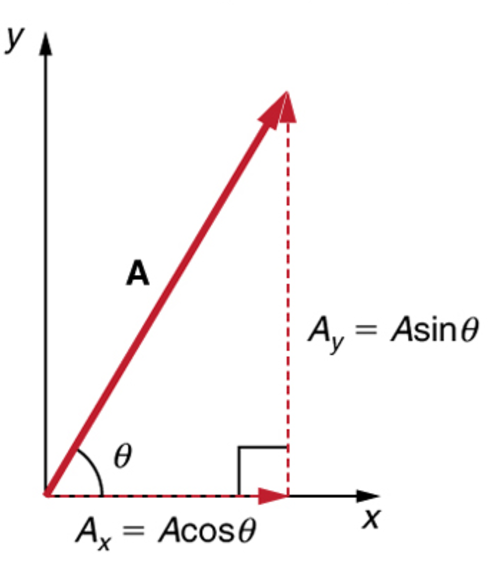
Vector addition and subtraction graphically:

To add two vectors, draw the first vector with its tail at the origin and then draw the second vector with its tail at the previous vectors head. Finally, draw a line from the origin to the head of the second vector. This line is the new vector, as shown below.

W= U+V

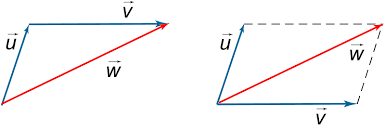
To subtract a vector, do the same as with addition but flip the vector which you are subtracting.

 

 

Practise Test

Here is a practise test I put together. It is 1hr long and made from V3 Past exam questions.

https://drive.google.com/file/d/1SxW4rSdmN5T4j08TqpJ9cBx3Py5JNOnI/view?usp=sharing

 

View count: 6488