Formulae

Name	Symbol	Formula
Gravitational force	F or W	$\frac{GMm}{r^2}$
Gravitational acceleration	g	$\frac{GM}{r^2}$
Gravitational potential energy	Ep	$-\frac{GMm}{r}$
Gravitational potential	V	$\frac{-GM}{r}$
Escape Velcocity	vesc	$\sqrt{\frac{2GM}{r}}$
Orbital velocity	vorbit	$\sqrt{\frac{GM}{r}}$

Describing Gravitational fields

gravitational potential energy: The work done against gravity to bring a small test mass from infinity to that point in space

gravitational potential: The work done against gravity per unit mass to bring a small test mass from infinity to that point in space.

gravitational force: The force exerted by gravity on a test mass at a point in space

gravitational field strength: The force exerted by gravity, per unit mass, on a test mass at a point in space $\frac{F}{m}$

What is a gravitational field?

All masses have an impact on the space around them. This influence is called a gravitational field. These fields allow us to predict how objects in space will interact, using vector fields. Gravitational fields are always attractive, they don't repel. The gravitational force will always act towards the centre of mass. 

We draw gravitational fields as shown below.

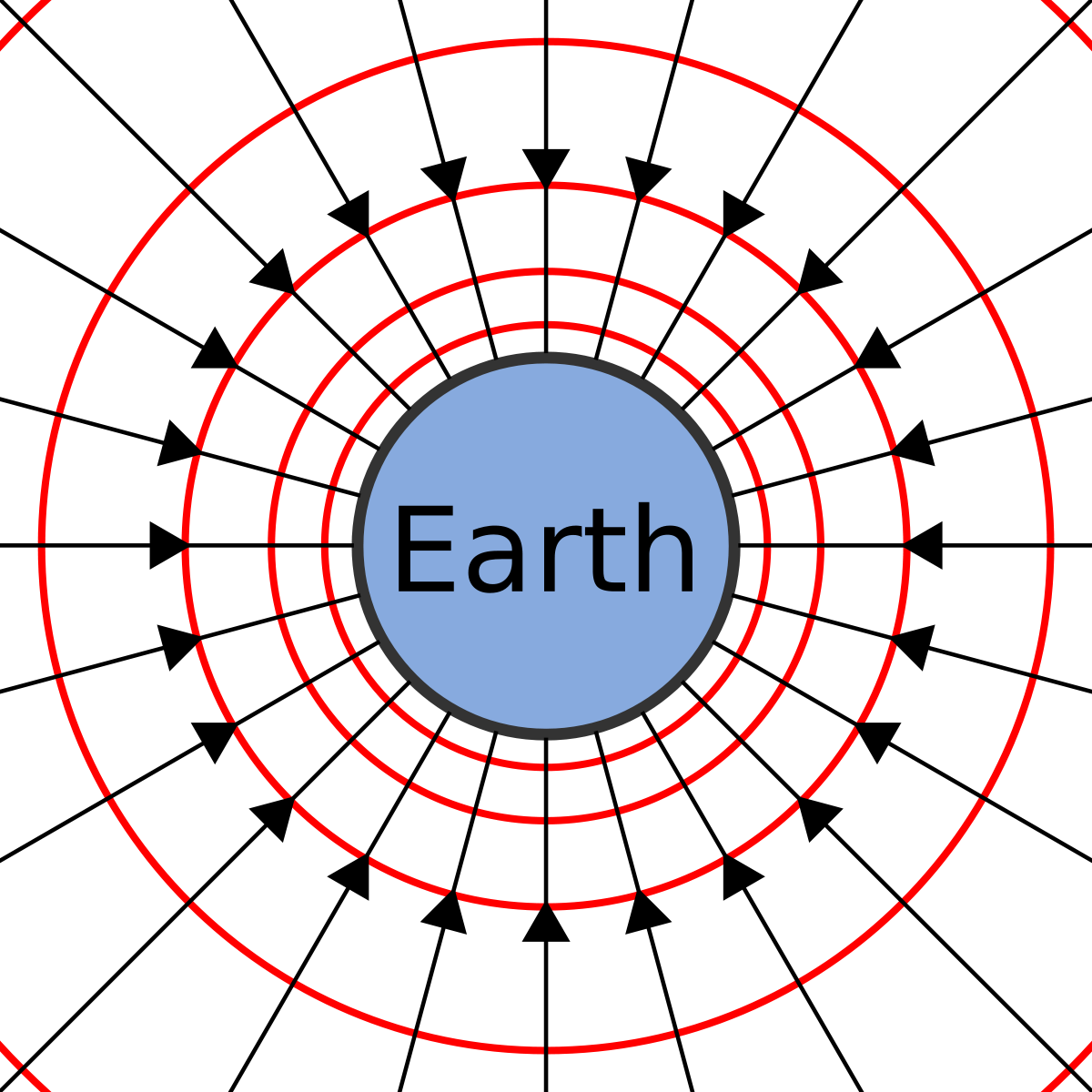
The arrows represent gravitational field lines. They show the direction of the gravitational field. If only one body is involved, these should always point towards the centre of mass. The density of the field lines indicates the strength of the gravitational field. (It's not a perfect proportionality, the density decreases linearly with distance from the centre of mass, but the magnitude of gravitational force decreases linearly with distance squared from the centre of mass. 

The red lines represent equipotential surfaces. Along these equipotential surfaces, potential energy is the same. Note that no work is done against gravity in moving a mass along these equipotential surfaces because the gravitational potential energy remains the same. These equipotential surfaces must always be perpendicular to the gravitational field lines. 

Gravitational Potential Energy for constant gravitational acceleration

The equation for work done by gravity on an object you might know is 

$W=mg\Delta h$

This comes from the equation for gravitational potential energy, which is 

$E_g=mgh$

And since work done by the field is equal to change in potential energy, we can get the first equation

 

Gravitational potential energy for non-constant gravitational acceleration

The problem with the equation E =mgh is that the gravitational acceleration isn't always constant. In fact, if work is done against or by the gravitational field, gravitational acceleration is never constant. (Though the change can be negligible). This is because when work is done by or against the gravitational field, there is a change in equipotential surfaces. This means the magnitude of the acceleration due to gravity has changed. When operating with gravitational fields, assuming that acceleration due to gravity is constant can lead to huge errors.

Deriving the formula for Gravitational potential Energy

An equation for gravitational potential energy for non-constant gravitational acceleration must be created. The best way to do this is to use the formula for gravitational acceleration in terms of radius from the centre of mass.

$g=\frac{GM}{r^2}$

Where M is the mass of the central planet, and r is the distance between the object and the centre of gravity. When we insert this formula into the equation for gravitational potential, we get the following

$E_{g_{}}=\frac{GMmh}{r^2}$

And since h is equal to r, we can change this to 

$E_g=\frac{GMm}{r}$

Why is potential energy negative?

Now comes the conceptually tricky part. The selected zero point (the point where potential energy is zero) is at r=infinity, where the gravitational field no longer has any effect. The advantage of choosing infinity as the zero point is that everyone in the universe has the same measuring scale. Remember that gravitational potential energy of an object at any point in a gravitational field is just the work done by gravity in moving the object from its location to the zero point. When the zero point is infinity, the object must be moved away from the centre of gravity. When this happens, work is done against gravity. It's as if gravity was doing negative work. This is the reason why gravitational potential energy is always negative. So the formula for gravitational potential when the zero point is infinity is

$E_g=-\frac{GMm}{r}$

Gravitational field strength vs gravitational potential proved with calculus

Gravitational field strength is actually just the negative rate of change of gravitational potential with respect to distance from the centre of gravity. A more normal way of writing this relation would be 

$g=-\frac{d{V}_g}{dr}=\frac{-∆V_g}{∆r}$

$V_g={\int }_{\infty }^{R}g dr = {\int }_{\infty }^R\frac{GM}{r^2}dr = -\frac{GM}{r}$

Variation of Gravitational Field strength with displacement from the Centre of Planet

Assuming a planet has a uniform density, the diagram below shows how acceleration due to gravity varies as one approaches the centre of gravity of a planet. You'll notice that the displacement is expressed in terms of R. R represents one planet radius. 

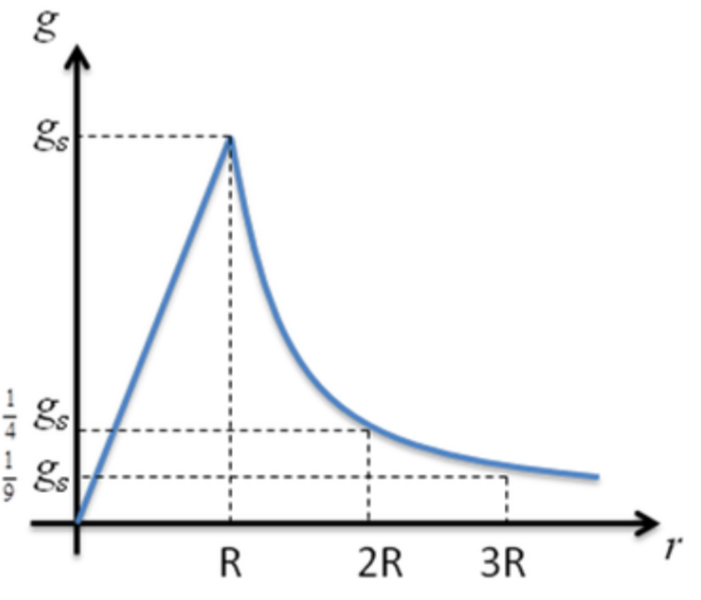
When the displacement is greater than R, things look as we'd expect. It's an inverse square relationship, the as the radius squared increases, the gravitational field strength decreases. This suits our equation for acceleration due to gravity. 

$g=\frac{GM}{r^2}$

Field strength when displacement is less than one radius

Things get trickier when the displacement is less that one radius of the planet. Acceleration due to gravity decreases linearly until it becomes 0. The reason for this is as you go under the surface of a planet, more and more of Earths mass is above you. The mass above you also attracts you, so the gravitational field strength decreases. 

Planets are obviously 3 dimensional. So as you approach the centre of one, the decrease in effective mass is a cubic relationship. The inverse square law is an inverse square relationship, so combining these two gives us a linear relationship, a direct proportionality. So gravitational field strength inside the planet is given by 

$g=\frac{r{g}_R}{R}$

Where g_R is the gravitational field strength at one radius R from the planet, and r is the distance from the centre of the planet. 

 

Gravitational fields at work

Escape speed

Escape speed: The minimum speed which will carry an object to infinity and bring it to rest there, hence allowing it to only just escape the gravitational pull.

To solve for escape speed, we are actually solving for when the velocity is high enough that it's kinetic energy is equal to its gravitational potential energy. This is because as the object travels from the planet the kinetic energy will turn into gravitational potential due to conservation of mechanical energy. So for kientic energy to be converted compeltely to gravitational potential by the time the mass reaches infinity, the two must be equal.

Deriving escape speed equation

change Kinetic energy = negative change gravitational energy

$$\begin{gathered} ∆E_k=-∆E_P \\ \frac{1}{2}m{v}^2=-\frac{-GMm}{r} \\ {v}^2=\frac{2GM}{r} so, V=\sqrt{\frac{{\displaystyle 2GM}}{{\displaystyle r}}} \end{gathered}$$

Kinetic energy orbiting satellite

In the unit: Circular motion and gravitation we derived the formula for orbital velocity. $V = \sqrt{\frac{GM}{r}}$ Now by substituting this in the kinetic energy equation we can get kinetic equation

$E_k=\frac{1}{2}\times m\times {\left(\sqrt{\frac{GM}{r}}\right)}^2=\frac{GMm}{2r}$

Total energy orbiting satellite

$$\begin{gathered} E_p=\frac{-GMm}{r} E_k=\frac{GMm}{2r} \\ {E}_t=E_p+E_k=\frac{-GMm}{r} +\frac{GMm}{2r} \\ {E}_t=\frac{-GMm}{2r} \end{gathered}$$

 

View count: 6107