Circular motion

Characteristics of Circular Motion

For an object in circular motion we define:

• The period, T, as the time taken to complete one revolution (seconds, s)
• The frequency, f, as the number of revolutions per second (hertz, Hz)

Remember $$1Hz=1s^−1$$, or one revolution per second.
These two variables are related through $f=1/T$.

Note that we often encounter different units when discussing the circular motion. For example, think of the rpm, (revolutions per minute) of engines, and the periods of planets in the Solar System expressed in years.

 

Angular velocity vs linear speed

Angular velocity: Change in angle per second. (Rad s^-1) Symbol = $\omega$

Linear speed: Change in distance of a point on the circumference per second. (ms^-1) Symbol = V

An object spinning can have a linear speed based on the distance a point on the circumference or an angular speed based on the angle. 

Since the circumference is given by $l=\theta \times r$ The linear velocity is $V=\omega r$

 

What are the characteristics of circular motion?

Uniform circular motion: Object with circular trajectory and constant angular velocity.

Circular motion is the type of motion that is undergone when a body curves around some 'point'. What's important here is that the distance between the body and the 'point' remains constant during the curve. It is very common in our world. For example, when a car goes around a corner, it is undergoing circular motion. Or when Earth orbits the sun, or when the moon orbits the Earth. These are all examples of circular motion. (They are actually elliptical orbits in real life but ignore this for this topic)

 

Centripetal force

When things move in circular motion they are changing direction constantly. From Newton's first law we know that if an object changes direction there is an external force present, therefore we know that there is force is being applied which causes the circular motion. The name of this force is a centripetal force. Centripetal force always points towards the center which is intuitive if you think about how you would keep an object moving in a circle. 

F = ma, therefore, F = mv^2 / r or and acceleration formula times the mass
Towards the center of the circle

There are many different types of force: drag, friction, gravitational, normal, tension, magnetic, electric, and other pushes and pulls between objects. Any of these forces can be centripetal.

All that 'centripetal' means is that the force is acting towards the center of the circle: it is a label for the particular force involved.

It is not yet another type of force to add to the list above. Hence, the centripetal force does not appear on a free body diagram, which only includes the physical forces acting on the object.

 

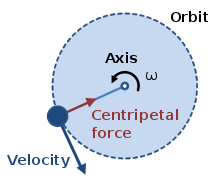
Centripetal acceleration

Centripetal acceleration: The acceleration the centripetal force causes towards the center.

The formula for centripetal acceleration: $a=\frac{v^2}{r}$ 

Always towards the center of the circle

There is no intuitive proof for this it is just obvious from experimental data. This relation means that the centripetal force is connected to your speed and your radius. You may not realize this but you will have seen this in real-life situations before. For example, if you turn a corner at high speeds a sharp corner (a small radius) is much harder than a wide turn (large radius) this is because the wider the turn the smaller the centripetal acceleration.

If you are given the period instead of the velocity, you can use a different equation (Both equations given in the formula book): $a=\frac{4{\mathrm{\pi }}^2\mathrm{r}}{T^2}$

With so many formulae linking various variables, uniform circular motion is a popular area in which examiners check your proportional reasoning in both Paper 1 and Paper 2. Use the IB Physics data booklet and pay close attention when rearranging and substituting.

 

Banking

Banking is when the slope an object moving along is angled causing the normal force to be angled and have a horizontal component. This horizontal component acts as part of the centripetal force. This is often used on roads with sharp turns or high-speed train lines, to help them make the turn without the wheels slipping by reducing the amount of force required by the tires, to keep turning. 

 

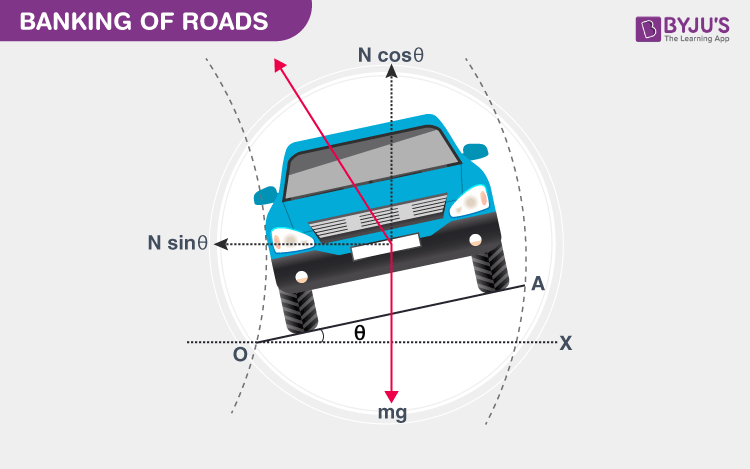
Gravitation

Newton's universal law of gravitation

Gravitational fields: regions of space where a mass experiences a force due to gravity.

Newton said that every single point mass attracts every other point mass with a force that is proportional to the product of their masses and inversely proportional to their separation. This can be expressed as a formula (In the formula book): $F=G\frac{Mm}{r^2}$

Where:

• G is the gravitational constant (6.67 x 10^-11 which is in the formula booklet)
• M is the larger mass
• m is the smaller mass
• r is the distance between the centers of two masses.

 

Bodies are assumed to be point masses

A uniform density body can be assumed to be just a point mass. If we assume planets are made of shells, everything cancels out to the center and we can assume it is a point mass. 

 

Gravitational field strength

This is the force (Newtons) per kilogram experienced by a test mass placed in the field. it is also known as the gravitational acceleration. 

Unit: N kg^-1 or ms^-2 (They mean the same thing)

Based on how force is mass * acceleration we get this equation $g =\frac{F}{m}$

 

Gravitational potential ($V_g$)

The work that is done per unit mass in bringing a small/point mass from infinity to a point (in the gravitational field);

 

Field Lines

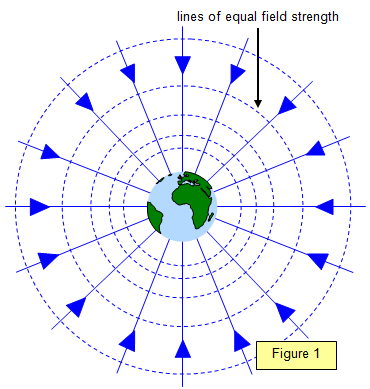
Field lines are a way of showing the direction and strength of the gravitational fields. They should be drawn pointing towards the center of mass, surrounding it in a circle. Only when the scale is very small can the lines be parallel. 

The field strength is represented by the field line density. The closer the lines the stronger the gravitational field strength.

 

Orbital Velocity

Recall that the acceleration of an object in a circular motion is  $a=\frac{v^2}{r}$ and that the acceleration of an object in orbit is $a = \frac{GM}{r^2}$

Therefore we can get an equation for the Velocity of an object in orbit, by rearranging:

$$\begin{gathered} \frac{v^2}{r}=\frac{GM}{r^2} \\ {v}^2=\frac{GM}{r} so V=\sqrt{\frac{{\displaystyle GM}}{{\displaystyle r}}} \end{gathered}$$

 

Escape velocity

To go from the surface of the planet to escape its gravitational field, to where potential is 0, the object has to travel to "infinity" away from that gravitational field. Because all energy has to be transferred, kinetic energy can be transformed into the potential energy needed to leave that field's attractive forces.

Change in potential energy = Change in kinetic energy

PE final - PE initial = KE initial - KE final

-GMm/ - (-GMm/r) = 1/2 mv² - 0

PE becomes so small it is negligible, and there is no more kinetic energy as it has been transferred into PE.

GMm/r = 1/2 mv²

GM/r = 1/2 v²

v² = 2GM/r

v =$\sqrt{\frac{2GM}{r}}$ 

NOTE: This is velocity is the ESCAPE velocity, not to be confused with ORBITAL velocity, which is; notice the factor. The escape velocity is directly upwards from the surface of the planet, while orbital velocity is perpendicular to this movement.

 

View count: 8732